I'm trying to calculate Euler-Lagrange equations for a robotic structure.
I'll use q to indicate the vector of the joint variables.
In my code, I use
syms t;
q1 = sym('q1(t)');
q2 = sym('q2(t)');
q = [q1, q2];
to declare that q1 and q2 depend on time t.
After I calculate the Lagrangian L (in this case it is a simple link with a rotoidal joint)
L = (I1z*diff(q1(t), t)^2)/2 + (L1^2*M1*diff(q1(t), t)^2)/8
The problem is that when I try to differentiate L respect to q using diff(L, q), I get this error
Error using sym/diff (line 69)
The second argument must be a variable or a nonnegative integer specifying the number of differentiations.
How can I differentiate L respect to q to have the first term of the Euler-Lagrange equation?
I also tried to write q simply as
syms q1 q2
q = [q1 q2]
without the time dependency but differentiation will not work, i.e. will obviously give me [0, 0]
That's what I've got in the workspace (I1z is the inertia of the link respect to z-axis, M1 is the mass of the link, L1 is the length of the link)
q = [q1(t), q2(t)]
diff(q, t) = [diff(q1(t), t), diff(q2(t), t)]
L = (I1z*diff(q1(t), t)^2)/2 + (L1^2*M1*diff(q1(t), t)^2)/8
If you want to run the full code, you have to download all the .m files from here and then use
[t, q, L, M, I] = initiate();
L = lagrangian(odof(q, L), q, M, I, t, 1)
otherwise the following code should be the same.
syms t I1z L1 M1
q1 = sym('q1(t)');
q2 = sym('q2(t)');
q = [q1, q2];
qp = diff(q, t);
L = (I1z*qp(1)^2)/2 + (L1^2*M1*qp(1)^2)/8;
EDIT
Thanks to AVK's answer I realized the problem.
Example 1 (AVK's code)
syms t q1 q2 q1t q2t I1z L1 M1 % variables
L = (I1z*q1t^2)/2 + (L1^2*M1*q1t^2)/8
dLdqt = [diff(L,q1t), diff(L,q2t)]
This will work and its result will be
dLdqt = [(M1*q1t*L1^2)/4 + I1z*q1t, 0]
Example 2 (wrong)
syms t q1 q2 q1t q2t I1z L1 M1
L = (I1z*q1t^2)/2 + (L1^2*M1*q1t^2)/8;
qt = [q1t q2t];
dLdqt = diff(L, qt)
This will not work, because diff expects a single variable of differentiation
Example 3 (right)
syms t q1 q2 q1t q2t I1z L1 M1
L = (I1z*q1t^2)/2 + (L1^2*M1*q1t^2)/8;
qt = [q1t q2t];
dLdqt = jacobian(L, qt)
This will work, because jacobian expects at least a variable of differentiation
EDIT 2
Seems that MATLAB's Symbolit Toolbox can't handle differentiation with respect to q(t), so you have to use the variable q.
So using these as functions
q = [q1(t), q2(t), q3(t), q4(t), q5(t), q6(t)]
qp = [diff(q1(t), t), diff(q2(t), t), diff(q3(t), t), diff(q4(t), t), diff(q5(t), t), diff(q6(t), t)]
and these as variables
qv = [q1, q2, q3, q4, q5, q6];
qvp = [q1p, q2p, q3p, q4p, q5p, q6p];
solved the problem.
The whole code will looks like this
syms q1 q2 q3 q4 q5 q6;
syms q1p q2p q3p q4p q5p q6p;
qv = [q1, q2, q3, q4, q5, q6];
qvp = [q1p, q2p, q3p, q4p, q5p, q6p];
Lagv = subs(Lag, [q, qp], [qv, qvp]);
dLdq = jacobian(Lagv, qv);
dLdqp = jacobian(Lagv, qvp);
dLdq = subs(dLdq, [qv, qvp], [q, qp]);
dLdqp = subs(dLdqp, [qv, qvp], [q, qp]);
m_eq = diff(dLdqp, t) - dLdq;
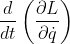later:
