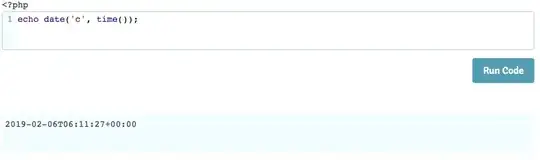
I have a GPS on the middle of a plate as can be seen in attached picture. Clearly, the GPS gives me the Lon. and Lat of the center of the plate with no problem.
My question is how can I estimate what is the Lon. and Lat at each end point (A,B,C,D) as the distance between end points and GPS is known? I believe there should be a formula for this purpose.
I appreciate any idea and suggestion in advance.
GPS and four points around it:
![][1]