Finding the centerpoint and boundaries of an arbitrary closed curve (random walk)

Question

Suppose you have an arbitrary closed curve (endpoint returns relatively close to first point) generated through a bunch of dataset coordinates, how do you find the centerpoint and the boundaries of the resulting shape?

Answer 1

There are two possible interpretations (perhaps more) for your question.

The first one was already addressed by @AakashM, and we may depict it in the following plot:

Where the red square is the "boundary".
I'll cite @AakashM here, because I understand his remark VERY important:"(I note that for you to have a closed curve, you need the endpoint to be not just 'close to', but coincident with the first point)"

As for the centerpoint, you have at least two "natural ways" for calculating it with this definitions:

1. Centerpoint = Middle Point of the Red Square
2. Centerpoint = { Mean of x coordinates of your curve, Mean of y coordinates of your curve}

Both of them may serve as a center point, but the results will be different.

The other way of dealing with the problem is finding the Convex Hull of your curve, as depicted below:

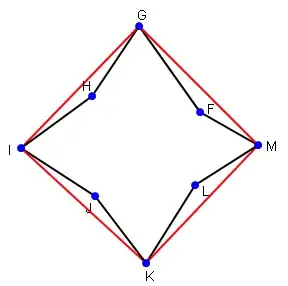
If you google for it, you will find algorithms for finding the Convex Hull, a nice introduction is here.

Again, you have two "natural ways for calculating the centerpoint:

1. Centerpoint = { Mean of x coordinates of your curve, Mean of y coordinates of your curve}
2. Centerpoint = { Mean of x coordinates of the CH points, Mean of y coordinates of the CH points}

HTH!

Answer 2

(I note that for you to have a closed curve, you need the endpoint to be not just 'close to', but coincident with the first point)

If by 'centerpoint' you mean center of mass, and you are assuming uniform density, then this question has what you want.

If by 'boundaries' you mean bounding rectangle with sides parallel to the axes, you just need the minimum and maximum x and y values on the curve.

If either of those aren't what you mean, please say...

Answer 3

For the boundaries, you can refer to the answers given by @belisarius and @AakashM.

As for centerpoint, you want "center of mass". Good 'ol Wikipedia has explanations and recipes at http://en.wikipedia.org/wiki/Center_of_mass and http://en.wikipedia.org/wiki/Centroid.

In general, you get a different result calculating the centroid than calculating the average of the vertices. This difference will be pronounced if the vertices are not uniformly distributed.