How to find nearest vector in {0,1,2}^12, over and over again

Question

I'm searching a space of vectors of length 12, with entries 0, 1, 2. For example, one such vector is
001122001122. I have about a thousand good vectors, and about a thousand bad vectors. For each bad vector I need to locate the closest good vector. Distance between two vectors is just the number of coordinates which don't match. The good vectors aren't particularly nicely arranged, and the reason they're "good" doesn't seem to be helpful here. My main priority is that the algorithm be fast.

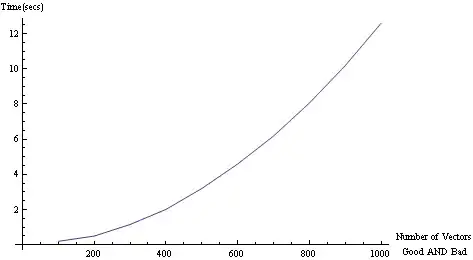
If I do a simple exhaustive search, I have to calculate about 1000*1000 distances. That seems pretty thick-headed.

If I apply Dijkstra's algorithm first using the good vectors, I can calculate the closest vector and minimal distance for every vector in the space, so that each bad vector requires a simple lookup. But the space has 3^12 = 531,441 vectors in it, so the precomputation is half a million distance computations. Not much savings.

Can you help me think of a better way?

Edit: Since people asked earnestly what makes them "good": Each vector represents a description of a hexagonal picture of six equilateral triangles, which is the 2D image of a 3D arrangement of cubes (think generalized Q-bert). The equilateral triangles are halves of faces of cubes (45-45-90), tilted into perspective. Six of the coordinates describe the nature of the triangle (perceived floor, left wall, right wall), and six coordinates describe the nature of the edges (perceived continuity, two kinds of perceived discontinuity). The 1000 good vectors are those that represent hexagons that can be witnessed when seeing cubes-in-perspective. The reason for the search is to apply local corrections to a hex map full of triangles...

Answer 1

Just to keep the things in perspective, and be sure you are not optimizing unnecessary things, the brute force approach without any optimization takes 12 seconds in my machine.

Code in Mathematica:

bad = Table[RandomInteger[5, 12], {1000}];
good = Table[RandomInteger[2, 12], {1000}];
distance[a_, b_] := Total[Sign@Abs[a - b]];

bestMatch = #[[2]] & /@ 
   Position[
    Table[Ordering@
      Table[distance[good[[j]], bad[[i]]], {j, Length@good}], {i, 
      Length@bad}], 1] // Timing

As you may expect, the Time follows a O(n^2) law:

Answer 2

This sounds a lot like what spellcheckers have to do. The trick is generally to abuse tries.

The most basic thing you can do is build a trie over the good vectors, then do a flood-fill prioritizing branches with few mismatches. This will be very fast when there is a nearby vector, and degenerate to brute force when the closest vector is very far away. Not bad.

But I think you can do better. Bad vectors which share the same prefix will do the same initial branching work, so we can try to share that as well. So we also build a trie over the bad vectors and sortof do them all at once.

No guarantees this is correct, since both the algorithm and code are off the top of my head:

var goodTrie = new Trie(goodVectors)
var badTrie = new Trie(badVectors)
var result = new Map<Vector, Vector>()
var pq = new PriorityQueue(x => x.error)
pq.add(new {good: goodTrie, bad: badTrie, error: 0})
while pq.Count > 0
  var g,b,e = q.Dequeue()
  if b.Count == 0: 
      //all leafs of this path have been removed
      continue
  if b.IsLeaf:
      //we have found a mapping with minimum error for this bad item
      result[b.Item] = g.Item
      badTrie.remove(b) //prevent redundant results
  else:
      //We are zipping down the tries. Branch to all possibilities.
      q.EnqueueAll(from i in {0,1,2}
                   from j in {0,1,2}
                   select new {good: g[i], bad: b[j], error: e + i==j ? 0 : 1})

return result   

A final optimization might be to re-order the vectors so positions with high agreement among the bad vectors come first and share more work.

Answer 3

3^12 isn't a very large search space. If speed is essential and generality of the algorithm is not, you could just map each vector to an int in the range 0..531440 and use it as an index into a precomputed table of "nearest good vectors".

If you gave each entry in that table a 32-bit word (which is more than enough), you'd be looking at about 2 MB for the table, in exchange for pretty much instantaneous "calculation".

edit: this is not much different from the precomputation the question suggests, but my point is just that depending on the application, there's not necessarily any problem with doing it that way, especially if you do all the precalculations before the application even runs.

Answer 4

My computational geometry is VERY rough, but it seems that you should be able to:

1. Calculate the Voronoi diagram for your set of good vectors.
2. Calculate the BSP tree for the cells of the diagram.

The Voronoi diagram will give you a 12th dimensional convex hull for each good vector that contains that all the points closest to that vector.

The BSP tree will give you a fast way to determine which cell a vector lies within and, therefore, which good vector it is closest to.

EDIT: I just noticed that you are using hamming distances instead of euclidean distances. I'm not sure how this could be adapted to fit that constraint. Sorry.

Answer 5

Assuming a packed representation for the vectors, one distance computation (comparing one good vector and one bad vector to yield the distance) can be completed in roughly 20 clock cycles or less. Hence a million such distance calculations can be done in 20 million cycles or (assuming a 2GHz cpu) 0.01 sec. Do these numbers help?

PS:- 20 cycles is a conservative overestimate.