I am trying to compute the derivative of some data and I was trying to compare the output of a finite difference and a spectral method output. But the results are very different and I can't figure out exactly why.
Consider the example code below
import numpy as np
from scipy import fftpack as sp
from matplotlib import pyplot as plt
x = np.arange(-100,100,1)
y = np.sin(x)
plt.plot(np.diff(y)/np.diff(x))
plt.plot(sp.diff(y))
plt.show()
This outputs the following result
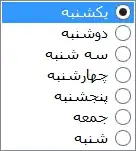
The orange output being the fftpack output. Nevermind the subtleties, this is just for the sake of an example.
So, why are they so different? Shouldn't they be (approximately) the same?
I'm pretty sure that the different amplitudes can be corrected with fftpack.diff's period keyword, but I can't figure which is the correct period (I thought it should be period=1 but that doesn't work).
Furthermore, how can I have my own spectral differentiation using numpy?