1

Snell's law states that the ratio of the sines of the angles of incidence and refraction is equivalent to the reciprocal of the ratio of the indices of refraction of given materials:

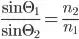
\frac{\sin{\Theta _{1}}}{\sin{\Theta _{2}}} = \frac{n _{2}}{n _{1}}

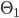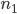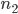I wanted to implement a simple program to visualize the law. Since \Theta _{1} , n _{1} and n _{1} are known, here's how I calculate \Theta _{2}:

theta2 = asin((sin(theta1) * n1) / n2);

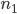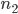The problem is that for certain values of n _{1} and n _{1} (for example 1.52 and 1.0 for glass and air respectively), the result of (sin(theta1) * n1) / n2 can be more than 1.0 for bigger angles, which makes asin return NaN. The way I cope with this is to check if (sin(theta1) * n1) / n2 is greater than 1.0 and if that's the case first subtract 1 from it, compute \Theta _{2} with the new value, then add 0.5 * M_PI (or 90.0 degrees) to it. Is there a better way?

  • Why do add the hack on for NaN values of `theta2`? Doesn't this correspond to total internal reflection? This is the case where there is no refracted ray. https://en.wikipedia.org/wiki/Snell's_law#Total_internal_reflection_and_critical_angle – Jonathan Chiang Feb 02 '17 at 20:37

1 Answers1

7

From the same Wikipedia page that you linked:

When light travels from a medium with a higher refractive index to one with a lower refractive index, Snell's law seems to require in some cases (whenever the angle of incidence is large enough) that the sine of the angle of refraction be greater than one. This of course is impossible, and the light in such cases is completely reflected by the boundary, a phenomenon known as total internal reflection.

So, you are doing it wrong. Checking if that value is higher than 1 is a good thing, if you want to avoid dealing with NaNs; but if it happens, by all means don't use some mathematical trick to circumvent that! It has a precise physical meaning, and that meaning must be kept!

Fabio says Reinstate Monica
  • 5,271
  • 9
  • 40
  • 61
  • Furthermore, you can use [Fresnel's equations](https://en.wikipedia.org/wiki/Fresnel_equations#Power_or_intensity_equations) to calculate the intensity of the reflected and transmitted (refracted) waves. – nibot Feb 21 '17 at 01:13