23

You can calculate skew and kurtosis with the the methods

However, there is no convenient way to calculate the coskew or cokurtosis between variables. Or even better, the coskew or cokurtosis matrix.

Consider the pd.DataFrame df

import pandas as pd
import numpy as np

np.random.seed([3,1415])
df = pd.DataFrame(np.random.rand(10, 2), columns=list('ab'))

df

          a         b
0  0.444939  0.407554
1  0.460148  0.465239
2  0.462691  0.016545
3  0.850445  0.817744
4  0.777962  0.757983
5  0.934829  0.831104
6  0.879891  0.926879
7  0.721535  0.117642
8  0.145906  0.199844
9  0.437564  0.100702

How do I calculate the coskew and cokurtosis of a and b?

piRSquared
  • 285,575
  • 57
  • 475
  • 624
  • **the current best answer is not correct** since it calculates the coskewness and cokurtosis matrix as square matrices. The coskewness and cokurtosis matrices are both tensors, which even when flattened would be rectangular arrays – develarist Dec 06 '20 at 12:50

1 Answers1

27

References

Calculating coskew

My interpretation of coskew is the "correlation" between one series and the variance of another. As such, you can actually have two types of coskew depending on which series we are calculating the variance of. Wikipedia shows these two formula

'left'
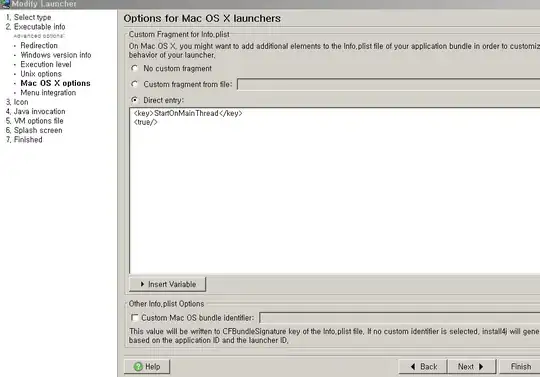
enter image description here
'right'
enter image description here

Fortunately, when we calculate the coskew matrix, one is the transpose of the other.

def coskew(df, bias=False):
    v = df.values
    s1 = sigma = v.std(0, keepdims=True)
    means = v.mean(0, keepdims=True)

    # means is 1 x n (n is number of columns
    # this difference broacasts appropriately
    v1 = v - means

    s2 = sigma ** 2

    v2 = v1 ** 2

    m = v.shape[0]

    skew = pd.DataFrame(v2.T.dot(v1) / s2.T.dot(s1) / m, df.columns, df.columns)

    if not bias:
        skew *= ((m - 1) * m) ** .5 / (m - 2)

    return skew

demonstration

coskew(df)

          a         b
a -0.369380  0.096974
b  0.325311  0.067020

We can compare this to df.skew() and check that the diagonals are the same

df.skew()

a   -0.36938
b    0.06702
dtype: float64

Calculating cokurtosis

My interpretation of cokurtosis is one of two

  1. "correlation" between a series and the skew of another
  2. "correlation" between the variances of two series

For option 1. we again have both a left and right variant that in matrix form are transposes of one another. So, we will only focus on the left variant. That leaves us with calculating a total of two variations.

'left'
enter image description here
'middle'
enter image description here

def cokurt(df, bias=False, fisher=True, variant='middle'):
    v = df.values
    s1 = sigma = v.std(0, keepdims=True)
    means = v.mean(0, keepdims=True)

    # means is 1 x n (n is number of columns
    # this difference broacasts appropriately
    v1 = v - means

    s2 = sigma ** 2
    s3 = sigma ** 3

    v2 = v1 ** 2
    v3 = v1 ** 3

    m = v.shape[0]

    if variant in ['left', 'right']:
        kurt = pd.DataFrame(v3.T.dot(v1) / s3.T.dot(s1) / m, df.columns, df.columns)
        if variant == 'right':
            kurt = kurt.T
    elif variant == 'middle':
        kurt = pd.DataFrame(v2.T.dot(v2) / s2.T.dot(s2) / m, df.columns, df.columns)

    if not bias:
        kurt = kurt * (m ** 2 - 1) / (m - 2) / (m - 3) - 3 * (m - 1) ** 2 / (m - 2) / (m - 3)
    if not fisher:
        kurt += 3

    return kurt

demonstration

cokurt(df, variant='middle', bias=False, fisher=False)

          a        b
a  1.882817  0.86649
b  0.866490  1.63200

cokurt(df, variant='left', bias=False, fisher=False)

          a        b
a  1.882817  0.19175
b -0.020567  1.63200

The diagonal should be equal to kurtosis

df.kurtosis() + 3

a    1.882817
b    1.632000
dtype: float64
piRSquared
  • 285,575
  • 57
  • 475
  • 624
  • Thank you very much for the detailed answer! worth an upvote :) Could you point to a real-world application of those that maybe doesn't have to do with high-level finance analysis, or at least something that isn't very abstract? I would be very interested in expert insights to get an intuition for those magnitudes – fr_andres Nov 30 '17 at 06:03
  • 1
    Skew of a dataset is a measure how non-symmetrical its distribution is (leans to left or right). You can envision this by maybe the mean of the distribution is pulled to the right due to an outlier while the median is not influenced. The mean would be to the right of the median in a right skewed distribution. It ends up being a measure of how related the difference of a datum with the mean is to the square of that difference. While co-skew is a measure of how related the difference of a datum with its mean is relative to the square of the difference of a datum in another dataset is to its – piRSquared Nov 30 '17 at 06:11
  • mean. Co-kurtosis has 2 interpretations. How related is one series' squared difference from its mean to another series squared difference to its mean. Or, the relationship of difference from mean relative to skew of another dataset. I apologize as I'm aware that this probably doesn't help clarify much. – piRSquared Nov 30 '17 at 06:13
  • I guess it doesn't get less abstract than that haha thank you anyway for your quick answer and insights – fr_andres Nov 30 '17 at 06:18
  • Well I guess I’ll have to go read ;-) and find out – piRSquared Dec 05 '20 at 15:15
  • **the code in this answer is not correct** since it calculates the coskewness and cokurtosis matrix as square matrices. The coskewness and cokurtosis matrices are both tensors, which even when flattened would be rectangular arrays, not square arrays – develarist Dec 06 '20 at 12:50
  • 1
    Feel free to add your own answer. – piRSquared Dec 06 '20 at 16:39