Assuming you have a array of discreet r and for each value of this array z(r). You want to fit a curve to estimate the parameters of an aspheric lens. I will use lmfit as mentioned here to show one way to do this using python.
Importing the modules used for this:
import numpy as np
import matplotlib.pyplot as plt
from lmfit import Model, Parameters
Define the function of an asperic lens:
def asphere_complete(x, r0, k, a2, a4, a6, a8, a10, a12):
r_squared = x ** 2.
z_even_r = r_squared * (a2 + (r_squared * (a4 + r_squared * (a6 + r_squared * (a8 + r_squared * (a10 + (r_squared * a12)))))))
square_root_term = 1 - (1 + k) * ((x / r0) ** 2)
zg = (x ** 2) / (r0 * (1 + np.sqrt(square_root_term)))
return z_even_r + zg
As you do not provide any data, I will use the following to create some example data, including artificial noise:
def generate_dummy_data(x, asphere_parameters, noise_sigma, seed=12345):
np.random.seed(seed)
return asphere_complete(x, **asphere_parameters) + noise_sigma * np.random.randn(x.shape[0])
The following function does the fitting and plots the resulting curve:
def fit_asphere(r, z, fit_parameters):
# create two subplots to plot the original data and the fit in one plot and the residual in another
fig, axarr = plt.subplots(1, 2, figsize=(10, 5))
fit_plot = axarr[0]
residuum_plot = axarr[1]
# configure first plot:
fit_plot.set_xlabel("r")
fit_plot.set_ylabel("z")
fit_plot.grid()
# configure second plot:
residuum_plot.set_xlabel("r")
residuum_plot.set_ylabel("$\Delta$z")
residuum_plot.grid()
# plot original data
fit_plot.plot(r, z, label="Input")
# create an lmfit model and the parameters
function_model = Model(asphere_complete)
# The fitting procedure may throw ValueErrors, if the radicand gets negative
try:
result = function_model.fit(z, fit_parameters, x=r)
# To plot the resulting curve remove the parameters which were just used for the constraints
opt_parameters = dict(result.values)
opt_parameters.pop('r_max', None)
opt_parameters.pop('radicand', None)
# calculate z-values of fitted curve:
z_fitted = asphere_complete(r, **opt_parameters)
# calculate residual values
z_residual = z - z_fitted
# plot fit and residual:
fit_plot.plot(r, z_fitted, label="Fit")
residuum_plot.plot(r, z_residual, label="Residual")
# legends:
fit_plot.legend(loc="best")
residuum_plot.legend(loc="best")
print(result.fit_report())
except ValueError as val_error:
print("Fit Failed: ")
print(val_error)
To set the parameters of the example data I use the Parametersobject of lmfit:
if __name__ == "__main__":
parameters_dummy = Parameters()
parameters_dummy.add('r0', value=-34.4)
parameters_dummy.add('k', value=-0.98)
parameters_dummy.add('a2', value=0)
parameters_dummy.add('a4', value=-9.67e-9)
parameters_dummy.add('a6', value=1.59e-10)
parameters_dummy.add('a8', value=-5.0e-12)
parameters_dummy.add('a10', value=0)
parameters_dummy.add('a12', value=-1.0e-19)
Create the example data:
r = np.linspace(0, 35, 1000)
z = generate_dummy_data(r, parameters_dummy, 0.00001)
The reason to use lmfitinstead of scipy's curve_fitis that the radicand of the square root may become negativ. We need to ensure:
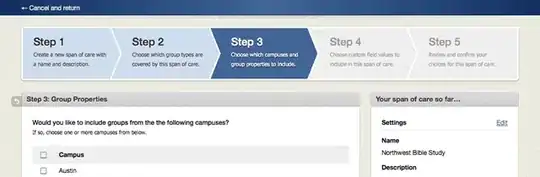
Therefor, we need to define a constraint as mentioned here.
Let's start to define our parameters we want to use in fitting. The basic radius is added straightforward:
parameters = Parameters()
parameters.add('r0', value=-30, vary=True)
To obey the inequality add a variable radicand which is not allowed to become less than zero. Instead of letting k taking part in the fitting normaly, make it direclty dependend on r0, r_max and radicand. We need to use r_max because the inequality is most problematic for the maximal r. Solving the inequalty for k leads to
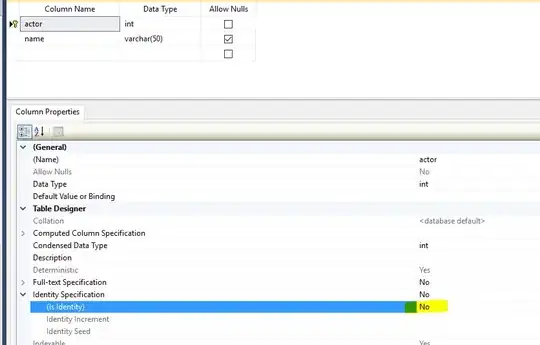
which is used as exprbelow. I use a bool flag to switch on/off the constraint:
keep_radicand_safe = True
if keep_radicand_safe:
r_max = np.max(r)
parameters.add('r_max', r_max, vary=False)
parameters.add('radicand', value=0.98, vary=True, min=0)
parameters.add('k', expr='(r0/r_max)**2*(1-radicand)-1')
else:
parameters.add('k', value=-0.98, vary=True)
The remaining parameters are added straightforward:
parameters.add('a2', value=0, vary=False)
parameters.add('a4', value=0, vary=True)
parameters.add('a6', value=0, vary=True)
parameters.add('a8', value=0, vary=True)
parameters.add('a10', value=0, vary=False)
parameters.add('a12', value=0, vary=True)
Now we are ready to start and get our results:
fit_asphere(r, z, parameters)
plt.show()
On the console you should see the output:
[[Variables]]
r0: -34.3999435 +/- 6.1027e-05 (0.00%) (init = -30)
r_max: 35 (fixed)
radicand: 0.71508611 +/- 0.09385813 (13.13%) (init = 0.98)
k: -0.72477176 +/- 0.09066656 (12.51%) == '(r0/r_max)**2*(1-radicand)-1'
a2: 0 (fixed)
a4: 7.7436e-07 +/- 2.7872e-07 (35.99%) (init = 0)
a6: 2.5547e-10 +/- 6.3330e-11 (24.79%) (init = 0)
a8: -4.9832e-12 +/- 1.7115e-14 (0.34%) (init = 0)
a10: 0 (fixed)
a12: -9.8670e-20 +/- 2.0716e-21 (2.10%) (init = 0)
With the data I use above, you should see the fit fail if keep_radicand_safe is set to False.


