Implementing the Izhikevich neuron model

Question

I'm trying to implement the spiking neuron of the Izhikevich model. The formula for this type of neuron is really simple:

v[n+1] = 0.04*v[n]^2 + 5*v[n] + 140 - u[n] + I

u[n+1] = a*(b*v[n] - u[n])

where v is the membrane potential and u is a recovery variable.

If v gets above 30, it is reset to c and u is reset to u + d.

Given such a simple equation I wouldn't expect any problems. But while the graph should look like , all I'm getting is this: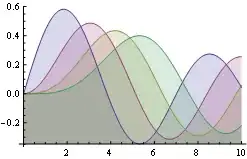

I'm completely at loss what I'm doing wrong exactly because there's so little to do wrong. I've looked for other implementations but the code I'm looking for is always hidden in a dll somewhere. However I'm pretty sure I'm doing exactly what the Matlab code of the author (2) is doing. Here is my full R code:

v = -70
u = 0
a = 0.02
b = 0.2
c = -65
d = 6
history <- c()

for (i in 1:100) {
  if (v >= 30) {
    v = c
    u = u + d
  }
  v = 0.04*v^2 + 5*v + 140 - u + 0
  u=a*(b*v-u); 
  history <- c(history, v)
}

plot(history, type = "l")

To anyone who's ever implemented an Izhikevich model, what am I missing?

usefull links: (1) http://www.opensourcebrain.org/projects/izhikevichmodel/wiki (2) http://www.izhikevich.org/publications/spikes.pdf

Answer

So it turns out I read the formula wrong. Apparently v' means new v = v + 0.04*v^2 + 5*v + 140 - u + I. My teachers would have written this as v' = 0.04*v^2 + 6*v + 140 - u + I. I'm very grateful for your help in pointing this out to me.

I saw this equation once... Isn't it v' instead of v[n+1]? So equation may looks like _v + 0.04*v^2 + 5*v + 140 - u_ . I tried implemented this model, but I have problem because coefitiens of differential equation have bad interaction with neuron input so there was liitle amount of spikes. Then I applied leaky integrate and fire model. — viceriel, Jan 20 '17 at 07:19
That's different notation for the same thing. v' and v[n+1] both mean "new value of v", v and v[n] both mean "old value of v". — Jumboman, Jan 20 '17 at 10:24
No. v[n+1] mean new value of _v_. _v'_ mean change of _v_ value. You replaced the _v_ with equation result but you need add equation result to _v_. — viceriel, Jan 20 '17 at 10:29
I think at @viceriel is right. If you look at the implementation in the original paper, the author appears to initialize the vector `v`, of length 1000, to -65 first and then within the loop `v=v+0.5*(0.04*v.^2+5*v+140-u+I)`. — emilliman5, Jan 20 '17 at 12:45
I see two problems. Wrong transcription of equations (Same thing with _u_) and voltage on neuron membrane is stimulated by external input(_I_), your is 0. — viceriel, Jan 20 '17 at 12:56
Oh man, I guess you are right. All my teachers use v' interchangably with v[n+1]... And I thought in the implementation it was some kind of matlab notation. I know about the input (should have mentioned that in the question). I was expecting just a straight line. — Jumboman, Jan 21 '17 at 16:35

score 2 · Accepted Answer · answered Jan 20 '17 at 18:33

Take a look at the code that implements the Izhikevich model in R below. It results in the following R plots:

Regular Spiking Cell:

Chattering Cell:

And the R code:

# Simulation parameters
dt = 0.01 # ms
simtime = 500 # ms
t = 0

# Injection current
I = 15
delay = 100 # ms

# Model parameters (RS)
a = 0.02
b = 0.2
c = -65
d = 8

# Params for chattering cell (CH)
# c = -50
# d = 2

# Initial conditions
v = -80 # mv
u = 0

# Input current equation
current = function()
{
  if(t >= delay)
  {
    return(I)
  }

  return (0)
}

# Model state equations
deltaV = function()
{
  return (0.04*v*v+5*v+140-u+current())
}

deltaU = function()
{
  return (a*(b*v-u))
}

updateState = function()
{
  v <<- v + deltaV()*dt
  u <<- u + deltaU()*dt

  if(v >= 30) 
  {
    v <<- c
    u <<- u + d
  }
}

# Simulation code
runsim = function()
{
  steps = simtime / dt
  resultT = rep(NA, steps)
  resultV = rep(NA, steps)

  for (i in seq(steps))
  {
    updateState()
    t <<- dt*(i-1)

    resultT[i] = t
    resultV[i] = v
  }

  plot(resultT, resultV, 
       type="l", xlab = "Time (ms)", ylab = "Membrane Potential (mV)")
}

runsim()

Some notes:

I've picked the parameters for the "Regular Spiking (RS)" cell from Izhikevich's site. You can pick other parameters from the two upper-right plots on that page. Uncomment the CH parameters to get a plot for the "Chattering" type cell.
As commenters have suggested, the first two equations in the question are incorrectly implemented differential equations. The correct way to implement the first one would be something like: "v[n+1] = v[n] + (0.04*v[n]^2 + 5*v[n] + 140 - u[n] + I) * dt". See the code above for example. dt refers to the user specified time step integration variable and usually dt << 1 ms.
In the for loop in the question, the state variables u and v should be updated first, then the condition checked after.
As noted by others, a current source is needed for both of these cell types. I've used 15 (I believe these are pico amps) from this page on the author's site (bottom value for I in the screenshot). I've also implemented a delay for the current onset (100 ms parameter).
The simulation code should implement some kind of time tracking so it's easier to know when the spikes are occurring in resulting plot. The above code implements this, and runs the simulation for 500 ms.

Thank you so much for this. I'm pretty sure my professors have always used v' to mean "new value of v" not "delta V", so that's where the problem was. I was also wondering when I should check the condition (ofc it only affects the graph, but it's important still). I should have mentioned I left the current at 0 on purpose (I was expecting a flat line and build from there). — Jumboman, Jan 21 '17 at 16:44
Glad I could help. Keep in mind that the code above is just one way to do numerical integration of diff eqs. There are other, more accurate methods out there. — Justas, Jan 21 '17 at 22:05
Oh I have one more question, just to be clear: It seems that when you calculate delta U, you are already using the updated value for v (or 'new' v)? or does the <<- assignment operator refer to the 'old' v? — Jumboman, Jan 21 '17 at 22:19
Generally, statements on the right side of the assignment operator are evaluated first and the resulting value is given to the variable on the left. Is this a homework question? If so, you should add the homework tag — Justas, Jan 21 '17 at 23:02
It's not homework, I'm doing some research for my thesis next year. I'm just not that familiar with R (my main programming language is Java). So I wonder why you are using <<- instead of the normal <- in this case. It looks like when you call deltaU(), in the function it uses the new value of V. But from what I gathered about <<- I wasn't sure if the earlier statement, v <<- v + deltaV()*dt, somehow creates a new variable v in the local scope, which would mean that the global variable v would still have the old value when you call deltaU(). — Jumboman, Jan 22 '17 at 13:07
The <<- operator is a global assignment operator in r. If it was replaced with <- or = there, the new value for v would not be assigned to the global v variable, and only kept locally within that function. In Java, you'd probably need to pass the v variable around as a parameter and could avoid using global vars. — Justas, Jan 22 '17 at 17:12

Implementing the Izhikevich neuron model

Answer

1 Answers1

Linked