Decay curve best fit SciPy

Question

I am having a problem when I try to find best fit to my data. Using scipy.optimize.curve_fit to create best fit. My data and code is:

EDIT You can download the data file from here. data is,

         a             b            b2
55478   1.07E+43    54395.93833 
56333   1.63E+43    54380.01385 
57540   2.57E+43    52393.31605 
61866   7.32E+43    52212.22838 52212.22838

code:

#!/usr/bin/env python
# -*- coding: utf-8 -*-


from __future__ import division

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import fit
import glob
import os
from scipy.optimize import curve_fit
import matplotlib.patches as patches

pf = pd.read_csv('/home/imhotep/Desktop/lala.csv', sep=',', encoding ='utf-8')



a1= pf['a'].max()
b1 = pf['b2'].max()
npoc=100

x = np.linspace((b1), (pf['b'].max()),npoc)
yy = np.linspace((pf['a'].min()), (pf['a'].max()), npoc)


fig = plt.figure()

ax4 = fig.add_subplot(111)

def h(x,k):
    return a1* (((x-(b1))/(k))**(-(5./3.)))


popt,pcov = curve_fit(h,x,yy)

print 'POPT,', popt,'PCOV',pcov
y_fi1 = h(x, *popt)

ax4.plot(x, y_fi1, label='fit', ls='-', color='blue')

ax4.plot(pf['b'], pf['a'], ls='None', color='blue', marker='o')

plt.show()

like that. When I run the code I'm getting that fit:

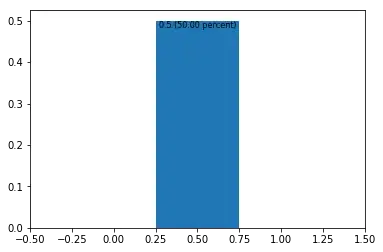
But, it should be roughly like that:

Can anyone tell me where I go wrong? I am beginner about curve fitting.

Answer 1

You want to fit a model to your 4 blue points described by a and b?

You should be doing fit in this direction then:

popt,pcov = curve_fit(h,b,a)

EDIT:

as mentioned in the comments of the question and this answer, you should be using the fit function only on your original data and then the newly created array using np.linspace to show the fit.

Here is what I got from your code:

#!/usr/bin/env python
# -*- coding: utf-8 -*-

from __future__ import division

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

pf = pd.read_csv('lala.csv', sep=',', encoding ='utf-8')

a1 = pf['a'].max()
#b1 = pf['b2'].max()

x = pf["b"]
y = pf["a"]

def h(x,k,b1):
    return a1*((x-b1)/k)**(-5/3)

popt,pcov = curve_fit(h,x,y)

print 'POPT,', popt,'PCOV',pcov

xfit = np.linspace(x.min(),x.max(),100)
y_fi1 = h(xfit, *popt)

fig = plt.figure()
ax4 = fig.add_subplot(111)
ax4.plot(xfit, y_fi1, label='fit', ls='-', color='blue')
ax4.plot(x, y, ls='None', color='blue', marker='o')
plt.show()

Using the curve_fit to find only parameter k resulted in an error, therefore I included b1 as a search parameter. Then it does find a fit, however still not completelly satisfying. The output:

POPT, [   238.09666313  51973.04601693] 
PCOV [[ 21500.32886377 -22370.88448044] [-22370.88448044  23850.34961769]]

Answer 2

You might try obtaining a better initial estimate of k by first linearising your equation in the old-fashioned way ...

... and then calculating a simple linear regression using the software of your choice. Here I used statsmodels to get 0.0007 for 1/k, implying an initial estimate of about 1400 for use with curve_fit.

import pandas as pd
import statsmodels.formula.api as smf
import statsmodels.api as sm
import matplotlib.pyplot as plt

df = pd.read_csv('lala.csv')
time_min = min(df.time)
luminosity_max = max(df.luminosity)
df['Y'] = (df.luminosity/luminosity_max)**(-0.6)
results = smf.ols('Y ~ time', data=df).fit()
print (results.summary())
fig, ax = plt.subplots()
fig = sm.graphics.plot_fit(results, 1, ax=ax)
plt.show()

From the error bars in the plot produced by this code it's obvious (if it wasn't otherwise) that there's considerable uncertainty in this estimate of k.

I still haven't succeeded in making curve_fit work. However, you might be interested in this modification to the function to be optimised. After renaming the columns in your csv (so the variables would be less confusing for me) I rewrote the main code in this way. I found that values for h around 1400 gave nan for the first time. I decided to simply replace these nan's with the maximum luminosity. If you run this I think you'll find that k=700 gives the best (crude) fit to start with.

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

df = pd.read_csv('lala.csv')
print (df)

luminosities = df.luminosity
times = df.time

luminosity_max= max(luminosities)
time_min = min(times)

def h(time,k):
    result = luminosity_max*((time-time_min)/k)**(-5./3.)
    if np.isnan(result):
        result = luminosity_max
    return result

for time in range(52000,56000,1000):
    print (time, h(time,2800), h(time,1400),h(time,700))

#~ popt,pcov = curve_fit(h,times,luminosities,700)
#~ print ('POPT,', popt,'PCOV',pcov)

Answer 3

I don't think you're doing anything wrong with curve_fit. I suspect that the mathematical model is a very poor fit for those data. Here's why. I ran the following code to calculate least-square error for various values of k.

import pandas as pd
import numpy as np

df = pd.read_csv('lala.csv')
print (df)

luminosities = df.luminosity
times = df.time

luminosity_max= max(luminosities)
time_min = min(times)

def h(time,k):
    result = luminosity_max*(max(time-time_min,5)/k)**(-5./3.)
    if np.isnan(result):
        result = luminosity_max
    return result

def LS(k):
    return sum([(luminosity-h(time,k))**2 for (luminosity,time) in zip(luminosities,times)])

for k in range(10,110,10):
    print (k, LS(k))

Results:

   dummy1  luminosity          time       dummy2
0   55478    1.066349  54395.938333          NaN
1   56333    1.630938  54380.013854          NaN
2   57540    2.569603  52393.316048          NaN
3   61866    7.324060  52212.228380  52212.22838
10 263.810260704
20 4431.42454446
30 18991.1298817
40 51557.4862318
50 110648.507655
60 205525.705606
70 346090.508811
80 542810.685895
90 806664.876933
100 1149099.00104

What I notice is that the smaller the value of k the smaller the LSE. But I think this would make the fitted model 'hug' the horizontal axis, as you saw.