1

(for the quick reader)

Question: Am I right that the Spectral analysis method to analyze a CHIRP is not so beneficial for parameter estimation/ model identification)

[EDIT]

My system is open-loop, 1 input (steering wheel angle) and 2 outputs (y-acceleration and yaw_Rate). To find vehicle characteristics I want to fit a linear transfer function to my data (Bicycle model). My current method is the 'Spectral analysis method': using test data to estimate the FRF and therefore the transfer function, because:

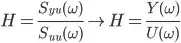
H = S_yu(\omega) / S_uu (w) --> H = Y(w)/U(w)

For dummy data (2 transfer functions excited by a chirp steering wheel angle) this works very well: accuracy of 99.98% to refit the model. For real test data, a real vehicle. this is nowhere near correct. Even if I average the data over 11 runs. Hence my confusion/question.

[will upload images of the test data tonight for clarification]

Background

I'm working on a project where I have to perform parameter identification of a car.

In simulator based compensatory tracking experiments I would excite the 'system' (read human) with a multi-sine signal and use the instrumental variable method (and function fitting) to perform system identification (Fourier transforming in- and output; and only evaluating the excited frequencies).

However, for a human driver this may be a bit difficult to do in the car. It is easier to provide sine-sweep (or CHIRP).

Unfortunately I think this input signal is not compatible with direct frequency domain analysis, because each frequency is only excited during a specific timeframe and the Foerier transform assumes a harmonic oscilation during the entire sample-time. I have checked some books (System Identification:A Frequency Domain Approach, System identification : an introduction and ) but can't seem to get a grip on how to use the CHIRP signal for the estimation of the Frequency Response Function (thus also the transfer function).

Alex
  • 114
  • 1
  • 6
Simon
  • 57
  • 1
  • 7

1 Answers1

1

Short answer (for the quick reader):

It depends on what you want to do. And yes, multisine signals can have favourable properties compared to chirps.

A bit longer answer:

You ask about chirp signals and their suitability for system identification / parameter estimation. Hence I assume you focus on frequency domain identification and hence I do not comment on time domain.

If you read the book "System Identification:A Frequency Domain Approach" by Pintelon/Schoukens (try to get the second edition from 2012), you will find (cf chapter 2) that the authors favour periodic signals over nonperiodic ones (like chirps) (and they do for good reasons, as periodic signals avoid major errors like leakage).

However if your system cannot be excited by periodic signals (for whatever reason), chirp signals may be a great excitation signal. In the aviation world, test pilots are even taught to perform good chirp signals. The processing of your data may be different for chirps (take a look at chapter 7 in the Pintelon/Schoukens book).

In the end there is just one thing that makes a good excitation signal - that is it gives the desired estimation result. If chirps work for your application: Go with them!

Unfortunately I think this input signal is not compatible with direct frequency domain analysis, because each frequency is only excited during a specific timeframe and the Foerier transform assumes a harmonic oscilation during the entire sample-time.

I do not understand what you mean with your this paragraph. Can you describe your problem in more detail?

P.S.: You didn't write much about your system. Is it static or dynamic? Linear / Nonlinear? Open loop or closed loop? SISO/MIMO? Are you limited to frequency domain ID? Can you repeat experiments? Each subject should be kept in mind when you decide about the excitation.

snowflake
  • 56
  • 7
  • Thank you very much for your time. My apologies for my delayed response. My system is a car, 1 input (steering wheel) 2 outputs yaw-rate and y-acc. Trying to find parameters, I want to fit a linear model to it (bicycle model), being limited to the chirp because that is all the data I am given. With dummy data I made myself I can estimate the transfer function with H = Y/U, however with real test data this is nowhere near accurate. Will update my question with the graphs I made (and the process so far). will re-check chapter 7 of that book, thank you. So far I have found no solution. – Simon Jan 11 '17 at 08:02
  • Thank you for your reply and your clarification. As far as I can tell, you seem to be on the right track and you use the right methods. However there are still many possible reasons that can cause poor estimation results, e.g. nonlinear effects, noise, etc. In [this case](http://dsp.stackexchange.com/a/31694/19747) the excitation signal was too short. Hope that helps. – snowflake Jan 17 '17 at 12:37