Directly Finding the Numerical Solution using integral:
Since you want to calculate H for different values of x, so instead of analytical solution, you can go for numerical solution.
Code:
syms y t;
f1=(1-exp(-y))/y; f2=-t+3*int(f1,[0,t]); f3=exp(f2);
H=integral(matlabFunction(f3),0,100) % Result of integration when x=100
Output:
H =
37.9044
Finding the Approximate Analytical Solution using Monte-Carlo Integration:
It probably is an "Elliptic Integral" and cannot be expressed in terms of elementary functions. However, you can find an approximate analytical solution using "Monte-Carlo Integration" according to which:
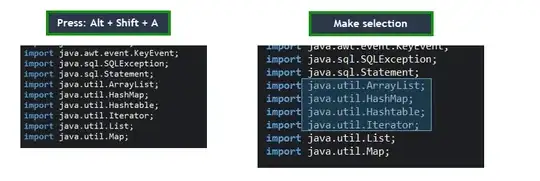
where f(c) = 1/n Σ f(xᵢ)
Code:
syms x y t;
f1=(1-exp(-y))/y; f2=-t+3*int(f1,[0,t]); f3=exp(f2);
f3a= matlabFunction(f3); % Converting to function handle
n = 1000;
t = x*rand(n,1); % Generating random numbers within the limits (0,x)
MCint(x) = x * mean(f3a(t)); % Integration
H= double(MCint(100)) % Result of integration when x=100
Output:
H =
35.2900
% Output will be different each time you execute it since it is based
% on generation of random numbers
Drawbacks of this approach:
- Solution is not exact but approximated.
- Greater the value of
n, better the result and slower the code execution speed.
Read the documentation of matlabFunction, integral, Random Numbers Within a Specific Range, mean and double for further understanding of the code(s).