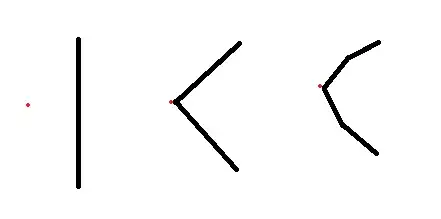Iteratively smooth a curve

Question

I've been trying to do this the whole day. Basically, I have a line and a point. I want the line to curve and pass through that point, but I don't want a smooth curve. I wan't to be able to define the number of steps in my curve, like so (beware crude mspaint drawing):

And so on. I tried various things, like taking the angle from the center of the initial line and then splitting the line at the point where the angle leads, but I have a problem with the length. I would just take the initial length and divide it by the number of steps I was at, but that wasn't quite right.

Anyone knows a way to do that?

Thanks.

Answer 1

You could go the other way around : first find a matching curve and then use the points on the curve to draw the lines. For example:

This plot was obtained in the following way:

Suppose you have the three starting points {x0,0},{x1,y1},{x2,0}

Then you find two parabolic curves intersecting at {x1,y1}, with the additional condition of having a maxima at that point (for a smooth transition). Those curves are:

 yLeft[x_] := a x^2 + b x + c; 
 yRight[x_] := d x^2 + e x + f;

Where we find (after some calculus):

   {c -> -((-x0^2 y1 + 2 x0 x1 y1)/(x0 - x1)^2), 
    a -> -(y1/(x0 - x1)^2), 
    b -> (2 x1 y1)/(-x0 + x1)^2}  

and

   {f -> -((2 x1 x2 y1 - x2^2 y1)/(x1 - x2)^2), 
    d -> -(y1/(x1 - x2)^2), 
    e -> (2 x1 y1)/(x1 - x2)^2}

so we have our two curves.

Now you should note that if you want your points equally spaced, x1/x2 should be a rational number.and your choices for steps are limited. You may chose steps passing by x1 AND x2 while starting from x0. (those are of the form x1/(n * x2))

And that's all. Now you form your lines according to the points {x,yLeft[x]} or {x,yRight[x]} depending upon on which side of x1 you are.

Note: You may chose to draw only one parabolic curve that pass by your three points, but it will result highly asymmetrical in the general case.

If the point x1 is in the middle, the results are nicer:

Answer 2

You would probably need to code this yourself. I think you could do it by implementing a quadratic bezier curve function in code, which can be found here. You decide how fine you want the increments by only solving for a few values. If you want a straight line, only solve for 0 and 1 and connect those points with lines. If you want the one angle example, solve for 0, 0.5, and 1 and connect the points in order. If you want your third example, solve for 0, 0.25, 0.5, 0.75, and 1. It would probably be best to put it in a for loop like this:

float stepValue = (float)0.25;
float lastCalculatedValue;
for (float t = 0; t <= 1; t += stepValue)
{
    // Solve the quadratic bezier function to get the point at t.
    // If this is not the first point, connect it to the previous point with a line.
    // Store the new value in lastCalculatedValue.
}

Edit: Actually, it looks like you want the line to pass through your control point. If that is the case, you don't want to use a quadratic bezier curve. Instead, you probably want a Lagrange curve. This website might help with the equation: http://www.math.ucla.edu/~baker/java/hoefer/Lagrange.htm. But in either case, you can use the same type of loop to control the degree of smoothness.

2nd Edit: This seems to work. Just change the numberOfSteps member to be the overall number of line segments you want and set the points array appropriately. By the way, you can use more than three points. It will just distribute the total number of line segments across them. But I initialized the array so that the result looks like your last example.

3rd Edit: I updated the code a bit so you can left click on the form to add points and right click to remove the last point. Also, I added a NumericUpDown to the bottom so you can change the number of segments at runtime.

public class Form1 : Form
{
    private int numberOfSegments = 4;

    private double[,] multipliers;
    private List<Point> points;

    private NumericUpDown numberOfSegmentsUpDown;

    public Form1()
    {
        this.numberOfSegmentsUpDown = new NumericUpDown();
        this.numberOfSegmentsUpDown.Value = this.numberOfSegments;
        this.numberOfSegmentsUpDown.ValueChanged += new System.EventHandler(this.numberOfSegmentsUpDown_ValueChanged);
        this.numberOfSegmentsUpDown.Dock = DockStyle.Bottom;
        this.Controls.Add(this.numberOfSegmentsUpDown);

        this.points = new List<Point> { 
            new Point(100, 110), 
            new Point(50, 60), 
            new Point(100, 10)};

        this.PrecomputeMultipliers();
    }

    public void PrecomputeMultipliers()
    {
        this.multipliers = new double[this.points.Count, this.numberOfSegments + 1];

        double pointCountMinusOne = (double)(this.points.Count - 1);

        for (int currentStep = 0; currentStep <= this.numberOfSegments; currentStep++)
        {
            double t = currentStep / (double)this.numberOfSegments;

            for (int pointIndex1 = 0; pointIndex1 < this.points.Count; pointIndex1++)
            {
                double point1Weight = pointIndex1 / pointCountMinusOne;

                double currentMultiplier = 1;
                for (int pointIndex2 = 0; pointIndex2 < this.points.Count; pointIndex2++)
                {
                    if (pointIndex2 == pointIndex1)
                        continue;

                    double point2Weight = pointIndex2 / pointCountMinusOne;
                    currentMultiplier *= (t - point2Weight) / (point1Weight - point2Weight);
                }

                this.multipliers[pointIndex1, currentStep] = currentMultiplier;
            }
        }
    }

    protected override void OnPaint(PaintEventArgs e)
    {
        base.OnPaint(e);

        Point? previousPoint = null;
        for (int currentStep = 0; currentStep <= numberOfSegments; currentStep++)
        {
            double sumX = 0;
            double sumY = 0;
            for (int pointIndex = 0; pointIndex < points.Count; pointIndex++)
            {
                sumX += points[pointIndex].X * multipliers[pointIndex, currentStep];
                sumY += points[pointIndex].Y * multipliers[pointIndex, currentStep];
            }

            Point newPoint = new Point((int)Math.Round(sumX), (int)Math.Round(sumY));

            if (previousPoint.HasValue)
                e.Graphics.DrawLine(Pens.Black, previousPoint.Value, newPoint);

            previousPoint = newPoint;
        }

        for (int pointIndex = 0; pointIndex < this.points.Count; pointIndex++)
        {
            Point point = this.points[pointIndex];
            e.Graphics.FillRectangle(Brushes.Black, new Rectangle(point.X - 1, point.Y - 1, 2, 2));
        }
    }

    protected override void OnMouseClick(MouseEventArgs e)
    {
        base.OnMouseClick(e);

        if (e.Button == MouseButtons.Left)
        {
            this.points.Add(e.Location);
        }
        else
        {
            this.points.RemoveAt(this.points.Count - 1);
        }

        this.PrecomputeMultipliers();
        this.Invalidate();
    }

    private void numberOfSegmentsUpDown_ValueChanged(object sender, EventArgs e)
    {
        this.numberOfSegments = (int)this.numberOfSegmentsUpDown.Value;
        this.PrecomputeMultipliers();
        this.Invalidate();
    }
}