I am a beginner at multilevel analysis and try to understand how I can do graphs with the plot functions from base-R. I understand the output of fit below but I am struggeling with the visualization. df is just some simple test data:
t <- seq(0, 10, 1)
df <- data.frame(t = t,
y = 1.5+0.5*(-1)^t + (1.5+0.5*(-1)^t) * t,
p1 = as.factor(rep(c("p1", "p2"), 10)[1:11]))
fit <- lm(y ~ t * p1, data = df)
# I am looking for an automated version of that:
plot(df$t, df$y)
lines(df$t[df$p1 == "p1"],
fit$coefficients[1] + fit$coefficients[2] * df$t[df$p1 == "p1"], col = "blue")
lines(df$t[df$p1 == "p2"],
fit$coefficients[1] + fit$coefficients[2] * df$t[df$p1 == "p2"] +
+ fit$coefficients[3] + fit$coefficients[4] * df$t[df$p1 == "p2"], col = "red")
It should know that it has to include p1 and that there are two lines.
The result should look like this:
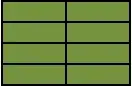
Edit: Predict est <- predict(fit, newx = t) gives the same result as fit but still I don't know "how to cluster".
Edit 2 @Keith: The formula y ~ t * p1 reads y = (a + c * p1) + (b + d * p1) * t. For the "first blue line" c, d are both zero.