I'm quite stuck at the moment with a little function I write. I want to embed the following function into my program:
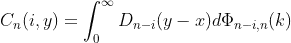
where 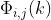 is the convolution of
is the convolution of 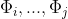 of the cumulative distribution function of a poisson distribution.
of the cumulative distribution function of a poisson distribution.
If I got it right, I'd calculate the convolution like this, where k is the number of events in an interval, Mu is just the mean e.g. 5 and j is the number of convolutions:
from scipy.stats import poisson
poisson.cdf(k, (Mu * (1 + i)))
The function D looks like this:
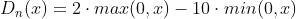
which is done in python like this:
def D(k, y, i):
y = y - k
return (2 * max(0, y) - 10 min(0, y)) * poisson.cdf(k, (Mu * (1 + i)))
Now the tricky part where I'm stuck is, how to get the integral to work with the cdf. Currently I'm trying to do it like this but I don't have a clue how to continue:
from scipy.integrate import quad
def Integrate(i, y):
return quad(D, 0, np.inf, args=(y, i))[0]
If anyone has an idea how to do that, I'd really appreciate it :)
Edit: To check whether the convolution of the cdf is correct, I did this:
print(poisson.pmf(0,(Mu * (1 + i))) + poisson.pmf(1,(Mu * (1 + i))))
>>> 0.445679641365
print(poisson.cdf(1,(Mu * (1 + i))))
>>> 0.445679641365