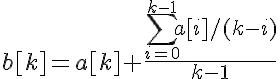Can I calculate an element without looping through all preceding elements in my case (see the question body)?

Question

I have 2 arrays of Doubles of the same length. Array a is filled with some data, array b is to be calculated.

Each element of the array b equals a corresponding value from array a plus a weighted sum of all preceding elements in the array b.

A weighted sum is calculated by adding all those elements each multiplied by a coefficient which equals its distance from the current element we calculate divided by number of elements in the preceding subset.

To implement this I loop through the whole preceding subset for each element I calculate.

Can this be optimized? I have not enough maths skills, but I suspect that I could only use the first preceding element to calculate every next as every element is already derived from the preceding set and contains all the information of it already weighted. Maybe I can just adjust the weight formula and get the same result without a second level looping?

This seems to be an example in Scala (I am not sure if it is correct :-]). As the real project uses negative indices, treat a(1) and a(2) as preceding a(0) in terms of the task written above.

import scala.Double.NaN
val a = Array[Double] (8.5, 3.4, 7.1, 5.12, 0.14, 5)
val b = Array[Double] (NaN, NaN, NaN, NaN, NaN, 5)
var i = b.length - 2
while (i >= 0) {
  b(i) = a(i) + {
    var succession = 0.0
    var j = 1
    while (i + j < b.length) {
      succession += b (i+j) * (1.0-j.toDouble/(b.length - i))
      j += 1
    }
    succession
  }
  i -= 1
}
b.foreach((n : Double) => println(n))

Answer 1

I assume the distance is the absolute difference of two elements.

If I understood it correctly each element of b has to be:

b(i) = a(i) + sum(j = 1 to i-1) (a(j) * (abs(a(i) - a(j)) / i )

b(i) = a(i) + sum(j = 1 to i-1) ( abs(a(j)*a(j) - a(j)*a(i)) / i )

Now, if we could write b(i+1) in terms of b(i) we would have done it.

The problem is that each weight depends on both, a(i) and a(j) (and even worse, it is the absolute difference).

That's why we can't simplify the above anymore and can't "extract" knowledge from each sum to use it in the next one.

Answer 2

That's what you're trying to do?

f(x_n) := g(x_0,..,x_(n-1)) + h(x_n)

The nested loop can only be optimized if we can find a equivalent function to replace g. Actually, I don't know the exact meaning of weighted sum. I guess, it's

g(x_0,..,x_(n-1)) = (x_0 + ... + x_(n-1)) / (n-1)

(adding all values and dividing by the number of values)

In that case, you could store the sum and reuse it:

a := (x_0 + ... + x_(n-2))
g(x_0,..,x_(n-1)) = (a + x_(n-1)) / (n-1)

This would eliminate the nested loop.

In terms of Java (implements my idea of a weighted sum):

double[] x = initX();
double[] y = new double[x.length];
double sum = 0;
y[0] = h(x[0]);
for (int i = 1; i < x.length; i++) {
  sum = sum + x[i-1];    
  y[i] = sum / (i-1) + h(x[i]);
}

Answer 3

Is this the equation for b?
(from http://texify.com/?$b[k]%20=%20a[k]%20+%20\frac{\sum_{i%20=%200}^{k%20-%201}{a[i]%20/%20(k-i)}}{k%20-%201}$)

Answer 4

You said:

by adding all those elements each multiplied by a coefficient which equals its distance from the current element we calculate

Most likely you can't predict the current element from the previous elements so you will at least have to compute those distances for each element: distance(i,j) where i < n and j < i. This means looping twice.

I think this could be optimized if distance was a linear function but conventionally a distance is non linear (so that it is positive). So my guess is that you'll have to loop twice.

Answer 5

There are three separate cases to consider.

(1) The weights don't change.

Example/solution:

val xs = List(1,2,3,4,5)
val ws = List(3,2,5,1,4)
// Desired:
  // 1
  // 1*3 + 2
  // 1*3 + 2*2 + 3
  // 1*3 + 2*2 + 3*5 + 4
  // 1*3 + 2*2 + 3*5 + 4*1 + 5
val mul = (xs,ws).zipped.map(_ * _)   // 1*3, 2*2, 3*5, etc.
val cuml = mul.scanLeft(0)(_ + _)     // Cumulative sums of the above
val ans = (xs,cuml).zipped.map(_ + _) // Put it all together

(2) The weights do change, but by a linear scaling factor as if they represent signed distances along a line. Then we let (d1-a)*x1 + (d2-a)*x2 + ... + (dn-a)*xn = y be our previous answer, assuming that we are at a; then if we move to b we can modify this as (d1-b)*x1... = (d1-a+a-b)*x1+... = (d1-a)*x1+(a-b)*x1+... which shows that we just need the sums of the x values and a single distance to get the new answer from our old ones. So:

val xs = List(1,2,3,4,5)
val ds = List(3,2,5,1,4)              // Treat these as distances along a line
// Desired:
  // 1
  // (3-2)*1 + 2
  // (3-5)*1 + (2-5)*2 + 3
  // (3-1)*1 + (2-1)*2 + (5-1)*3 + 4
  // (3-4)*1 + (2-4)*2 + (5-4)*3 + (1-4)*4 + 5
val ws = ds.map(_ - ds.head)          // Distances from the first element
val mul = (xs,ws).zipped.map(_ * _)
val cuml = mul.scanLeft(0)(_ + _)
// If we used this alone we would get:
  // 1
  // (3-3)*1 + 2            <-- should be subtracting 2, not 3!
  // (3-3)*1 + (2-3)*2 + 3  <-- should be subtracting 5, not 3!
  // etc.
val cumlx = xs.scanLeft(0)(_ + _)             // Need this to fix up our sums
val fix = (cumlx,ws).zipped.map(-1 * _ * _)   // This will actually do it
val ans = (xs,cuml,fix).zipped.map(_ + _ + _)

The best way to understand how this works is to take it apart statement by statement and write things out by hand to verify that it is actually computing what we want it to compute.

(3) The weights change in no consistent manner as you advance. Distances to points in a plane tend to have that property, since the nonlinearity of the square root basically means that you have to calculate each one over again. So you just have to do the whole calculation each time.