Race Car Puzzle

Question

Could you please help me with this puzzle that I am not able to find a nice answer to!!

There are 49 cars which race at unique speeds. Also there is a race track in which at maximum 7 cars can be raced together. We need to find the 25th fastest car in the group. We don't have a stop watch to measure time (so we can only measure the relative speed of each car w.r.t the 6 other cars in a race). What is the least number of races that would be needed?

Answer 1

Following Dialecticus inspiration. Divide into 7 random groups and race each of them, then race the medians of these groups. This car becomes the pivot and we already know its relation to 30 other cars, directly or indirectly (this is a property of the median of medians). So to place it with resp. the other 18 we need to run 3 races all including the pivot. After the pivoting, we need to recurse on at most 33 cars. Keep going. I ended up with 29 races. Even if you assume that complete sorting is needed, which is not, there is a lower bound at 17 races (a true lower bound will be even lower), which is much less than 29. So I suspect this is not the right answer, but since this has been lacking any solution, here is a suboptimal one. If you look at the research on sorting networks (this problem with races limited to two cars at a time), finding optimal networks is difficult and optimal networks are known only for very small sizes, definitely not up to 49. I am not aware of any research on networks with 7-way comparators.

Maybe an example can help. Let's say number the cars from the slowest to the fastest and arrange them in a 7x7 matrix (arbitrarily, since we don't know speeds until we race them).

     [,1] [,2] [,3] [,4] [,5] [,6] [,7]
[1,]   34   25   45   43   26   21   13
[2,]   11   24    2   40   14   30   32
[3,]   27   19   29   42    4   17   46
[4,]   15   10   39   33    1    9    5
[5,]   28   18   41    8   23   20    6
[6,]   16    3   38    7   12   22   36
[7,]   31   44   48   35   49   37   47

Then let's race each of the columns and sort them according to the outcome of the race:

     [,1] [,2] [,3] [,4] [,5] [,6] [,7]
[1,]   11    3    2    7    1    9    5
[2,]   15   10   29    8    4   17    6
[3,]   16   18   38   33   12   20   13
[4,]   27   19   39   35   14   21   32
[5,]   28   24   41   40   23   22   36
[6,]   31   25   45   42   26   30   46
[7,]   34   44   48   43   49   37   47

Now let's race row #4 (medians) and rearrange the columns according to the outcome

     [,1] [,2] [,3] [,4] [,5] [,6] [,7]
[1,]    1    3    9   11    5    7    2
[2,]    4   10   17   15    6    8   29
[3,]   12   18   20   16   13   33   38
[4,]   14   19   21   27   32   35   39
[5,]   23   24   22   28   36   40   41
[6,]   26   25   30   31   46   42   45
[7,]   49   44   37   34   47   43   48

Now observe that the median of medians (element [4,4]) is faster than any car above and left and slower than any car below and right (this is a property of the median of medians). For the other cars (lower left and upper right) we don't know, so we need to race them against [4,4], 6 at a time (3 races). Now we observe that 26 cars are slower than [4,4] and therefore the median must be one of those. No need to race any of the others any further. Now repeat the process with those 26 cars.

Answer 2

I have a solution that requires only 17 races.

First, though, let me explain a simple solution that requires 32 races. Divide the cars into 7 groups of 7, and race each group (7 races). Repeat 25 times: Pick the fastest remaining car from each group and enter it into a race, and set aside the winner (25 races). The first of the 25 races determines the fastest overall car (#1), the second race determines #2, and so on.

Now a solution with only 17 races:

Our strategy will be to first identify the 24 fastest cars (let's call these cars "speedy"). Then we'll find the fastest of the rest (#25).

Randomly place the cars on a 7x7 grid, and race each row (7 races). Then, race the 3rd place finishers from each race (8th race), and sort the rows by the 3rd place finisher speeds.

So, after 8 races we have this:

Each grid cell represents a car. An arrow points to the faster car. Note that the arrow is transitive.

Already we can identify 8 "speedy" cars:

How do we know they are speedy? Take a look at the blue 'x'. Only 23 cars are possibly faster than it (those not in the bottom-right 5x5). So, it is certainly "speedy". You can verify this for the other x's.

We have identified 8 of the 24 "speedy" cars. Let's remove these 8 from future consideration. We are now looking for the fastest 16 of the remaining cars. Our seven groups have sizes 4,4,5,7,7,7, and 7. (For the diagrams, whenever we remove a car, let's slide the remaining cars in the row to the left.)

Let's race the 2nd fastest remaining car of each group, and sort the rows accordingly (9th race). As before, we can identify 4 cars which are certainly among the 16 fastest (i.e. "speedy"):

I colored in the cells where the removed cars might be, but this has no effect yet.
We have identified 12 "speedy" cars. Remove the "speedy" cars, and we look for the fastest 12 of the remaining cars. Our groups have sizes between 2 and 7. Let's race the 2nd fastest remaining car of each group, and sort the rows accordingly (10th race). We identify 2 cars which are among the 12 fastest (i.e. "speedy"):

(10 "speedy" cars remain.)

We can repeat the previous step twice more (11th and 12th races). Each time we remove 2 more cars. However, note that a row/group might have 0 or 1 cars in it. If it has 1 car in it, we race that car instead of "the 2nd fastest remaining". If that car wins, we know that it is "speedy", as well as the next fastest 2nd place car. In any case we identify 2 "speedy" cars. (6 "speedy" cars remain.)

After 12 races we have identified and removed 18 "speedy" cars. We need to identify the remaining 6 "speedy" cars.

Now let's simply race the fastest remaining car in each group (13th race), and sort the rows accordingly. The winner is "speedy". 5 left.

After that last race, there are only 2 cars which could be the fastest remaining car. The blue o's:

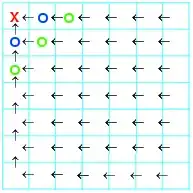
Additionally, the 2nd fastest remaining car is either a blue 'o' or green 'o'. Let's race these 5 cars (14th race), and the top two finishers are certainly "speedy". 3 left.

Let's repeat the last two steps/races to identify the last 3 speedy cars (15th and 16th race).

So, we have identified 24 "speedy" cars. The fastest remaining car must be the 25th fastest. We can find this car by simply racing the fastest car in each row/group (17th race).

Answer 3

Try one of these algorithms

http://en.wikipedia.org/wiki/Quick_select

Answer 4

http://www.sureinterview.com/shwqst/1062001

Round one

1. (7 races) Divide the cars into 7 groups and get the order within each group.
2. (1 race) Take the 7 medians and get the order. Find the median of medians (denote as o). In following example, it is 34.
3. (3 races) Find the rank of the median of medians. Take 6 elements from lower-left corner (25 ~ 33) and upper-right corner (13 ~ 21) and race against the o (34). After 3 rounds, we know the rank of this median of medians within in the whole set. The best case is that o is the global median (25th fastest). The worst case is that o is the 16th or 34th fastest.

This example shows one possible worst case.

1   2   3   4   13  14  15  <- group 1
5   6   7   8   16  17  18 
9   10  11  12  19  20  21     ...
22  23  24  34  35  36  37
25  26  27  38  39  40  41  <- group 5
28  29  30  42  43  44  45  <- group 6
31  32  33  46  47  48  49  <- group 7

Round two

We want to find the rank of other medians in a binary search fashion.

1. (3 races) Pick the median less than 34, which is 12. Race it against the lower-left and upper-right corner cars. After 3 races, we know its rank is 12.

Now, the gap between those two medians are at most 21, as shown in this example.

Round three

Rearrange the 21 cars (>12 and <34) as follows.

13  14  15  <- group 1
16  17  18 
19  20  21     ...
22  23  24
25  26  27  <- group 5
28  29  30  <- group 6
31  32  33  <- group 7

Each row is still sorted.

1. (1 race) Find the median of medians again, which is 23.
2. (1 race) Find its rank. After this step, we know the car in previous step is ranked 23 for sure.
3. (1 race) Similar to a binary search, check the rank of another median, 29.
4. (1 race) Sort all cars between 23 ~ 29 (exclusive). The 25th fastest car is found.

So at most 18 races are needed to get the 25th fastest car.

Answer 5

Can't you iteratively divide the pool by determining the exact position of a car?

Pick a car at random to pivot by Run through each of the other 48 cars, racing them in groups of 6 against the pivot car You know now the pivot car's exact position.

Now run the same process on the portion of the set that you know to include position 25 in it. If you have less than seven elements in the remaining partition, it is simple to determine.

The worst case performance of this is truly horrendous, but could be mitigated by picking successive pivots in some semi-intelligent way.

Answer 6

You can always solve it in 8 races... Lets take a Pivot Car say Car1 and race it with all other cars in 8 races and take the relative speed of other cars wrt Car1. lets say the result is given below: Read Car#(Relative speed to Car1)

---

Race 1: Car1-(0), Car2-(+10), Car3(+5), Car4(+7), Car5(-3), Car6(-4), Car7(+1)

Race 2: Car1-(0), Car8-(+10), Car9(+5), Car10(+7), Car11(-3), Car12(-4), Car13(+1)

Race 3: Car1-(0), Car14-(+11), Car15(+4), Car16(+6), Car17(-4), Car18(-10), Car19(+2)

Race 4: Car1-(0), Car20(+9), Car21(+3), Car22(+5), Car23(-5), Car24(-11), Car25(+3)

Race 5: Car1-(0), Car26-(+8), Car27(+2), Car28(+6), Car29(-6), Car30(-12), Car31(+4)

Race 6: Car1-(0), Car32-(+7), Car33(+1), Car34(+3), Car35(-7), Car36(-13), Car37(+5)

Race 7: Car1-(0), Car38-(+6), Car39(-1), Car40(+2), Car41(-8), Car42(-14), Car43(+6)

Race 8: Car1-(0), Car44-(+5), Car45(-2), Car46(+1), Car47(-9), Car48(-15), Car49(+7)

Since Car1 is the pivot car and the speed of each car is consistent through all the races, we can group all the results togather.

If you sort the relative speed (wrt car1) you can find out the 25th fastest car.