11

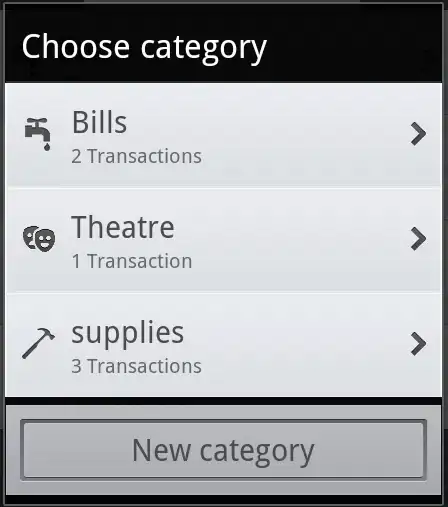
I'm reading an image segmentation paper in which the problem is approached using the paradigm "signal separation", the idea that a signal (in this case, an image) is composed of several signals (objects in the image) as well as noise, and the task is to separate out the signals (segment the image).

The output of the algorithm is a matrix, S \in R^{MxT} which represents a segmentation of an image into M components. T is the total number of pixels in the image, s_{ij} is the value of the source component (/signal/object) i at pixel j

In the paper I'm reading, the authors wish to select a component m for m \in [1,M] which matches certain smoothness and entropy criteria. But I'm failing to understand what entropy is in this case.

Entropy is defined as the following:

H(s_m) = - \sum_{n=1}^{256} p_n (s_m) \cdot log_2 (p_n (s_m)), m= 1,..., M

and they say that ''{p_n(s_m)}_​{n=1}^{256} are probabilities associated with the bins of the histogram of s_m''

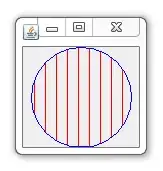The target component is a tumor and the paper reads: "the tumor related component s_m with "almost" constant values is expected to have the lowest value of entropy."

But what does low entropy mean in this context? What does each bin represent? What does a vector with low entropy look like?

link to paper

Cœur
  • 37,241
  • 25
  • 195
  • 267
user7154564
  • 113
  • 1
  • 1
  • 5

3 Answers3

13

They are talking about Shannon's entropy. One way to view entropy is to relate it to the amount of uncertainty about an event associated with a given probability distribution. Entropy can serve as a measure of 'disorder'. As the level of disorder rises, the entropy rises and events become less predictable.

Back to the definition of entropy in the paper:

Definition of entropy in the paper

H(s_m) is the entropy of the random variable s_m. Here Probability term is the probability that outcome s_m happens. m are all the possible outcomes. The probability density p_n is calculated using the gray level histogram, that is the reason why the sum runs from 1 to 256. The bins represent possible states.

So what does this mean? In image processing entropy might be used to classify textures, a certain texture might have a certain entropy as certain patterns repeat themselves in approximately certain ways. In the context of the paper low entropy (H(s_m) means low disorder, low variance within the component m. A component with low entropy is more homogenous than a component with high entropy, which they use in combination with the smoothness criterion to classify the components.

Another way of looking at entropy is to view it as the measure of information content. A vector with relatively 'low' entropy is a vector with relatively low information content. It might be [0 1 0 1 1 1 0]. A vector with relatively 'high' entropy is a vector with relatively high information content. It might be [0 242 124 222 149 13].

It's a fascinating and complex subject which really can't be summarised in one post.

Tapio
  • 1,502
  • 1
  • 12
  • 24
  • 1
    MacKay is good on this topic (http://www.inference.org.uk/itprnn/book.html). Could one use entropy in the sense of information content to quantify image quality, e.g. how blurred an image is? – jtlz2 Apr 27 '18 at 15:41
  • 1
    Hmm, maybe? How blurred compared to what? The total entropy of an image will vary order of magnitudes depending on what's in the image, so as a knee jerk reaction I'd guess that even slightly different image contents would dominate any change caused by a realistic amount of blurriness. On the other hand it seems like people apply K-L divergence fairly succesfully to almost everything nowadays, so if you got a standard candle texture or image then why not? My first instict would be to look at some frequency based techniques though. – Tapio Apr 28 '18 at 17:01
3

Entropy was introduced by Shanon (1948), were the higher value of Entropy = more detailed information. Entropy is a measure of image information content, which is interpreted as the average uncertainty of information source. In Image, Entropy is defined as corresponding states of intensity level which individual pixels can adapt. It is used in the quantitative analysis and evaluation image details, the entropy value is used as it provides better comparison of the image details.

Abdullah Jirjees
  • 53
  • 6
1

Perhaps, another way to think about entropy and information content in an image is to consider how much an image can be compressed. Independent of the compression scheme (run length encoding being one of many), you can imagine a simple image having little information (low entropy) can be encoded with fewer bytes of data while completely random images (like white noise) cannot be compressed much, if at all.

user11490381
  • 21
  • 1