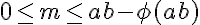0

In Q-learning, from its current state, the agent takes action at every discrete time step and after an action is performed, an agent receives an immediate reward to access the success or failure of performed action. Let's say that we want to control a vehicle speed using Q-learning where the actions are target speeds and agent's goal is to reach stop-line (which is 1km away from the starting point) as quickly as possible.

1) So in this example, does agent need to take action at every discrete time step (1sec) or agent can get an action at every 100m instead of every discrete time step. Is that a must to take action at every discrete time step?

2) what is mean by delayed reward in Q-learning? is that updating reward once agent reaches to the target instead of updating reward after taking each action at every time step? Thanks in advance :)

D_Wills
  • 345
  • 1
  • 3
  • 14

1 Answers1

2

1) does agent need to take action at every discrete time step (1sec) or agent can get an action at every 100m instead of every discrete time step. Is that a must to take action at every discrete time step?

I think you may be confusing the concept of time step in Q-learning with our physical realization of time. In Q-learning, each time step is a time when it's the agent's turn to make a move/take an action. So if the game is chess, then every time step would be when it's the player's time to play. So how frequent your agent can take an action is decided by the rules of the game. In your example, it's not quite clear to me that what the rules of the "game" are? If the rules say the agent gets to pick an action every 1 "second", then the agent will need to follow that. If you think that's too frequent, you can see if "None" is an available action option for the agent to take or not.

what is mean by delayed reward in Q-learning? is that updating reward once agent reaches to the target instead of updating reward after taking each action at every time step?

To understand delayed reward, perhaps take a look at the formula would help.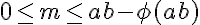Q-learning formula As you can see, the Q value at time step t is not only impacted by the old Q value and immediate reward but also by the "estimated optimal future value". This estimated optimal value (with a hyperparameter discount factor to be tuned) is set to capture the "delayed reward".

The intuition behind delayed reward is that sometimes one action may seem to be a bad action to take at that time (mathematically by taking this action the agent received a low immediate reward or even penalty), but somehow this action leads to a long term benefit. Put it in your example, assume the agent is at position P, there are two routes to get to the stop-line. One route has a straight distance of 1 km, the other has a bit of detour and has a distance of 1.5 km. The agent takes the 1.5 km route, it would perhaps receive less immediate reward than picking the 1 km route. Let's further assume that the 1.5 km route has a higher speed limit than the 1 km route, which actually leads the agent to get to the stop line faster than taking the 1 km route. This "future reward" is the delayed reward which needs to be taken into account when calculating the Q value of (state at position P , action of taking 1.5 km route) at time step t.

The formula could be a bit confusing to implement since it involves a future Q value. The way I did it once was simply computing the Q-value at time step t without worrying about the delayed reward. 

# @ time step t
Q(st, at) = Q(st, at) + alpha * immedate_reward - alpha*Q(st, at)

Then after reaching time step t+1, I went back to update the previous Q-value at time step t with delayed reward.

# @ time step t+1
Q(st+1, at+1) = Q(st+1, at+1) + alpha * immedate_reward - alpha*Q(st+1, at+t)
Q(st, at) = Q(st, at) + alpha * gama * max(Q(st+1, a))

I hope this helps clarify and answers your question...

Zhongyu Kuang
  • 5,104
  • 2
  • 25
  • 26
  • Thank you very much for the explanations. Now i got a clear understanding about the updating time -step. – D_Wills Oct 19 '16 at 07:00
  • @ Zhongyu Kuang . – D_Wills Oct 19 '16 at 07:00
  • Regarding the delay reward, – D_Wills Oct 19 '16 at 07:10
  • regarding the delayed reward, the major advantage of the Q-learning method is (TD methods) is that you does not need to know the reward values for each transition. So if I update the Q-value function after taking each action with the immediate reward and estimated future optimal value, Isn't that violating the fundamental advantage of Q-learning ? Lets say that along the lkm agent gets 5 actions (10km/h,20km/h,40km/h,60km,h and 50km/h).. so should i wait until agent reach to the goal state to update the Q-value function? Or can I update it immediately after taking each action? – D_Wills Oct 19 '16 at 07:17
  • "Transition" and "state" are different concepts in reinforcement learning. "Transition" would be a function of state @ time step t and then take action @ time step t and then land in another state @ t+1. However, if you look at the Q-learning function, Q-value is plainly a function of state and action at a time step, it doesn't care which other state you land in after taking an action. In your example, you should update Q-value after taking every action. – Zhongyu Kuang Oct 19 '16 at 14:02
  • Assume you initialize all Q(state, action) with 1, after taking action of 60 km/h at time step 0, you update Q(state0, action0) with Q(state0, action0) + alpha * immedate_reward - alpha*Q(state0, action0). This action takes the agent to another state1 at time step 1. Then you do two things. (1) You update Q(state1, action1) = Q(state1, action1) + alpha * immedate_reward - alpha*Q(state1, action1). (2) now you can estimate the optimal future values for the previous Q(state0, action0). This may seem counterintuitive, but remember the method assumes that agent visits each state infinite times. – Zhongyu Kuang Oct 19 '16 at 14:06
  • Therefore after "infinite" times of visiting state0, you would have a set of Q-values of at this state corresponding to taking a set of different actions. And b/z Q-value has taken into account of the delayed reward that each action would lead you to in the future, this max(Q(st+1, a)) term in the formula becomes a more and more accurate estimate of "long term gain" (of course assuming if you tuned the discount factor appropriately) – Zhongyu Kuang Oct 19 '16 at 14:13