I am trying to implement gradient descent algorithm to minimize the objective of hinge loss of SVM. The equation I am trying to implement is
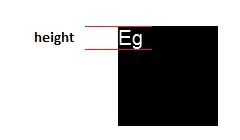
and max function is handled by sub gradient technique as below.
The issue is I am not able to get proper convergence. Every time I run the code, the weights w turn out to be different.
Below is python implementation
import sys;
import random;
## Helper function
## Dot_product : calculates dot product
## of two vectors in argument
def dot_product(a,b):
result = [];
for col in range(0,len(a),1):
t = a[col]*b[col];
result.append(t);
return sum(result)
dataset=[];
dataset = [[1,1], [1,2], [1,3], [3,1], [3,2], [3,3], [50,2]]
label_dictionary ={'2': -1.0, '1': -1.0, '4': 1.0, '3': 1.0, '0': -1.0, '5': 1.0, '6': 1.0}
cols = len(dataset[0]);
rows = len(dataset);
w = []
for i in range(0, cols, 1):
w.append(random.uniform(-1, 1))
print('W = ', w)
# gradient descent
eta = 0.01;
error = 2;
iterations = 1;
difference = 1;
delf = [0]*cols;
#for i in range(iterations):
while(difference > 0.001):
#print('Starting gradient descent.');
for row_index in range(rows):
if str(row_index) in label_dictionary:
# calculate delf
xi = dataset[row_index];
yi = label_dictionary.get(str(row_index))
dp = dot_product(w,xi); # w*xi
condition = dp*yi;
# Sub gradient. Diff of max.
if(condition < 1):
for col in range(cols):
delf[col] += -1*xi[col]*yi;
elif(condition>=1):
delf = [0]*cols;
# Update
for j in range(0, cols, 1):
w[j] = w[j] - eta * delf[j];
# Compute error
#print('W',w);
prev = error;
error = 0;
for i in range(0, rows, 1):
dp = dot_product(w, dataset[i]);
if str(i) in label_dictionary:
yi = int(label_dictionary[str(i)]);
error += (yi - dp) ** 2
difference = prev - error;
print('Error',difference)
print('W ',w)
# Predictions
# row labels that are not in
# dictionary
## Start Predictions
## if rowindex is not in labels dictionary
## that is our test sample
for index,x in enumerate(dataset):
if(str(index) not in label_dictionary):
#print('Testing data found', index, x)
dp = dot_product(w,x);
if(dp > 0):
print(1,index);
else:
print(0,index);