Fast optimization of "pathological" convex function

Question

I have a simple convex problem I am trying to speed up the solution of. I am solving the argmin (theta) of

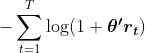
where theta and rt is Nx1.

I can solve this easily with cvxpy

import numpy as np
from scipy.optimize import minimize
import cvxpy

np.random.seed(123)

T = 50
N = 5
R = np.random.uniform(-1, 1, size=(T, N))

cvtheta = cvxpy.Variable(N)
fn = -sum([cvxpy.log(1 + cvtheta.T * rt) for rt in R])

prob = cvxpy.Problem(cvxpy.Minimize(fn))
prob.solve()

prob.status
#'optimal'

prob.value
# -5.658335088091929

cvtheta.value
# matrix([[-0.82105079],
#         [-0.35475695],
#         [-0.41984643],
#         [ 0.66117397],
#         [ 0.46065358]])

But for a larger R this gets too slow, so I am trying a gradient based method with scipy's fmin_cg:

goalfun is a scipy.minimize friendly function that returns the function value and the gradient.

def goalfun(theta, *args):
    R = args[0]
    N = R.shape[1]
    common = (1 + np.sum(theta * R, axis=1))**-1

    if np.any( common < 0 ):
        return 1e2, 1e2 * np.ones(N)

    fun = np.sum(np.log(common))

    thetaprime = np.tile(theta, (N, 1)).T
    np.fill_diagonal(thetaprime, np.ones(N))
    grad = np.sum(np.dot(R, thetaprime) * common[:, None], axis=0)

    return fun, grad

Making sure the function and gradients are correct:

goalfun(np.squeeze(np.asarray(cvtheta.value)), R)
# (-5.6583350819293603,
#  array([ -9.12423065e-09,  -3.36854633e-09,  -1.00983679e-08,
#          -1.49619901e-08,  -1.22987872e-08]))

But solving this just yields garbage, regardless of method, iterations, etc. (The only things that yields Optimization terminated successfully is if x0 is practically equal to the optimal theta)

x0 = np.random.rand(R.shape[1])

minimize(fun=goalfun, x0=x0, args=R, jac=True, method='CG')
#   fun: 3.3690101669818775
#      jac: array([-11.07449021, -14.04017873, -13.38560561,  -5.60375334,  -2.89210078])
#  message: 'Desired error not necessarily achieved due to precision loss.'
#     nfev: 25
#      nit: 1
#     njev: 13
#   status: 2
#  success: False
#        x: array([ 0.00892177,  0.24404118,  0.51627475,  0.21119326, -0.00831957])

I.e. this seemingly innocuous problem that cvxpy handles with ease, turns out to be completely pathological for a non-convex solver. Is this problem really that nasty, or am I missing something? What would be an alternative to speed this up?

Did you try the solver [SCS](https://github.com/cvxgrp/scs) (within cvxpy), probably with ```use_indirect=True``` mode? — sascha, Oct 12 '16 at 18:54
No, I haven't set any solver options, everything I ran is as it is in the example above, I assumed the default options where fine here? — luffe, Oct 12 '16 at 18:56
Sure, default uses ECOS which is good. SCS is sometimes **much** faster while beeing a bit less accurate (ADMM-based method). There are two modes, where one is something like a truncated-newton method. (SCS compiled from sources will be much faster than the default one; multithreading). There is even GPU-support. **UPDATE** ecos:90secs; scs=3 secs for 5000x500 (source-install with MT; use_indirect=True). — sascha, Oct 12 '16 at 18:58
Thank you `prob.solve(solver='SCS', use_indirect=True)` gave me a speedup, but it was not in your order of magnitude (but I haven't tried installing from source with mt yet) — luffe, Oct 12 '16 at 19:10

Stelios · Accepted Answer · 2016-10-12T18:59:09.997

2

I believe the issue is that it is possible for theta to be such that the log argument becomes negative. It seems that you have identified this issue, and have goalfun return the tuple (100,100*ones(N)) in this case, apparently, as a heuristic attempt to suggest the solver that this "solution" is not preferable. However, a stronger condition must be imposed, i.e., this "solution" is not feasible. Of course, this can be done by providing appropriate constraints. (Interestingly, cvxpy appears to handle this issue automatically.)

Here is a sample run, without bothering with providing derivatives. Note the use of a feasible initial estimate x0.

np.random.seed(123)

T = 50
N = 5
R = np.random.uniform(-1, 1, size=(T, N))

def goalfun(theta, *args):
    R = args[0]
    N = R.shape[1]
    common = (1 + np.sum(theta * R, axis=1))**-1

    return np.sum(np.log(common))

def con_fun(theta, *args):
    R = args[0]

    return 1+np.sum(theta * R, axis=1)


cons = ({'type': 'ineq', 'fun': lambda x: con_fun(x, R)})

x0 = np.zeros(R.shape[1])
minimize(fun=goalfun, x0=x0, args=R, constraints=cons)

 fun: -5.658334806882614
 jac: array([ 0.0019, -0.0004, -0.0003,  0.0005, -0.0015,  0.    ])  message: 'Optimization terminated successfully.'
nfev: 92
 nit: 12
njev: 12   status: 0  success: True
   x: array([-0.8209, -0.3547, -0.4198,  0.6612,  0.4605])

Note that when I run this, I get an invalid value encountered in log warning, indicating that at some point in the search a value of theta is checked which barely satisfies the constraints. However, the result is reasonably close to that of cvxpy. It would be interesting to check if the cvxpy solution changes when the constraints are explicitly imposed in the cvxpy.Problem formulation.

edited Oct 12 '16 at 18:59

answered Oct 12 '16 at 18:51

Stelios

5,271
1
18
32

Yes, I return a large positive number for values that are not in the valid domain, I thought this was common heuristic for these types of problems? And yes `cvxpy` is much more elaborate, the `cvxpy.log` function is a complex object that (as far as I understand) take care of the valid domain – luffe Oct 12 '16 at 18:59
So is Is doing this (restricting the domain) with `cons_fun` the prefered procedure? Thank you – luffe Oct 12 '16 at 19:06
@luffe You are essentially applying a "penalty" method, where the problem domain is implicitly imposed by altering the objective function. However, this is a heuristic approach, which, in general, does not guarantee that the resulting solution will be the same as in the case where the domain is explicitly imposed. Penalty methods are typically applied when the domain specification is complicated (i.g., many non-linear inequalities). In this case, the domain specification is very simple (linear inequalities). – Stelios Oct 12 '16 at 19:08
Ah, I see. But when I copy and paste your example, I only get `Iteration limit exceeded'` (restarted my IPython (2) sesson). Thank you – luffe Oct 12 '16 at 19:18
@luffe Works fine for me, both with Python 2 and 3 (`scipy.__version__` 0.18.1) – Stelios Oct 12 '16 at 19:28
That is very strange, if I create a blank Python 2 notebook on `juliabox.com` and copy and paste this I get `IndexError: tuple index out of range`. If I set `args=(R,),` I still get a `Desired error not necessarily achieved due to precision loss.'`. Thank you – luffe Oct 12 '16 at 21:20
It works for me using scipy 17.1, but it stillt gives some warnings regarding the log and it will be much slower than cvxpy + scs-indirect for higher-dimensions (at least for all of my tests). – sascha Oct 12 '16 at 22:29
Strange, maybe this is OSX specific, b/c I tried the above code on two windows machines and that went fine, but I get the same error on another Mac – luffe Oct 13 '16 at 16:55
@Stelios: In your optimization output: the `x` array is `5x1` like it should be, but the jacobian `jac` is `6x1`, the same happens here, very strange... – luffe Oct 14 '16 at 11:15
@Stelios Wow, this is perhaps a bug manifesting itself in differences in some machine precision between OSs, if I change the constraint func to `.99 + np.sum(theta * R, axis=1)` this gives me the right result. with `1` instead of `.99` this gives `'Iteration limit exceeded'`. – luffe Oct 14 '16 at 11:47
@luffe I'm not sure if it' relevant here. But for me, the code probably uses Intel's MKL as i'm using an anaconda distribution. On Mac OX X it's typically binding to Accelerate. – sascha Oct 14 '16 at 23:26

Fast optimization of "pathological" convex function

1 Answers1