I'm working on a personal project to create a simple 3D rendering program. So far it can render simple solids such as cubes, cuboids, tetrahedrons, etc...

The program works by providing a set of (CCW ordered) vertices which are then triangulated using a Delanuay algorithm. I'm not using any third party libraries and everything was been written in VB.NET from scratch... and I'm assuming the algorithms are properly implemented.
Here's the code that provides the vertices for a cube (yes, I'm aware that the actual length of the resulting solid will be 2 * length):
Public Shared Function Cube(length As Double) As List(Of Point3d)
' G-----F
' /| /|
' B-----A |
' | H---|-E
' |/ |/
' C-----D
Dim A As New Point3d(length, length, -length)
Dim B As New Point3d(-length, length, -length)
Dim C As New Point3d(-length, -length, -length)
Dim D As New Point3d(length, -length, -length)
Dim E As New Point3d(length, -length, length)
Dim F As New Point3d(length, length, length)
Dim G As New Point3d(-length, length, length)
Dim H As New Point3d(-length, -length, length)
Return New List(Of Point3d) From {A, B, C, D, E, F, G, H}
End Function
For the case of the sphere, I figured I could generate a set of vertices for a 180° arc on the XY plane and then rotate this arc along the X axis. Unfortunately, it appears that the Delaunay algorithm creates an invalid solid that doesn't meet Euler's formula for closed surfaces: V - E + F = 2

Here's the code that is supposed to generate the vertices for the sphere:
Public Shared Function Sphere(radius As Double) As List(Of Point3d)
Dim vertices As New List(Of Point3d)
Dim arc As New List(Of Point3d)
Dim p As New Point3d(0, 0, 0)
Dim angleStep As Double = 45.0
For ca As Double = 0.0 To 180.0 Step angleStep
arc.Add(New Point3d(radius * Math.Cos((ca - 180.0) * Point3d.ToRad),
radius * Math.Sin((ca - 180.0) * Point3d.ToRad),
0))
Next
vertices.AddRange(arc)
Dim v As Point3d
For ax As Double = 0 To 360.0 Step angleStep
For i As Integer = 0 To arc.Count - 1
v = arc(i).RotateX(ax)
Dim isDuplicate As Boolean = False
For j As Integer = 0 To vertices.Count - 1
If vertices(j).IsSimilar(v) Then
isDuplicate = True
Exit For
End If
Next
If Not isDuplicate Then vertices.Add(v)
Next
Next
Return vertices
End Function
Interestingly enough, if I set the angle step for each vertex to 90° the program, as expected, produces a valid octahedron. But reducing the angle step, in order to have a sphere with more faces, produces an invalid solid.
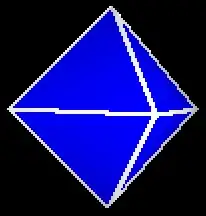
So... the question is: what am I doing wrong?
UPDATE (2016/10/10): I've published the complete source code on GitHub: https://github.com/morphx666/3DEngine