How to perform a non linear regression for my data

Question

I have set of Temperature and Discomfort index value for each temperature data. When I plot a graph between temperature(x axis) and Calculated Discomfort index value( y axis) I get a reversed U-shape curve. I want to do non linear regression out of it and convert it into PMML model. My aim is to get the predicted discomfort value if I give certain temperature.

Please find the below dataset :

Temp <- c(0,5,10,6 ,9,13,15,16,20,21,24,26,29,30,32,34,36,38,40,43,44,45, 50,60)

Disc<-c(0.00,0.10,0.25,0.15,0.24,0.26,0.30,0.31,0.40,0.41,0.49,0.50,0.56, 0.80,0.90,1.00,1.00,1.00,0.80,0.50,0.40,0.20,0.15,0.00)

How to do non linear regression (possibly with nls??) for this dataset?

Answer 1

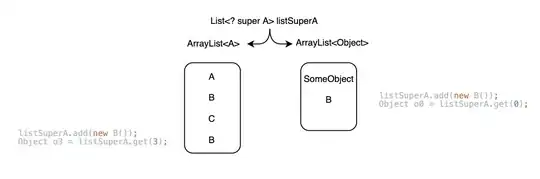
I did take a look at this, then I think it is not as simple as using nls as most of us first thought.

nls fits a parametric model, but from your data (the scatter plot), it is hard to propose a reasonable model assumption. I would suggest using non-parametric smoothing for this.

There are many scatter plot smoothing methods, like kernel smoothing ksmooth, smoothing spline smooth.spline and LOESS loess. I prefer to using smooth.spline, and here is what we can do with it:

fit <- smooth.spline(Temp, Disc)

Please read ?smooth.spline for what it takes and what it returns. We can check the fitted spline curve by

plot(Temp, Disc)
lines(fit, col = 2)

Should you want to make prediction elsewhere, use predict function (predict.smooth.spline). For example, if we want to predict Temp = 20 and Temp = 44, we can use

predict(fit, c(20,44))$y
# [1] 0.3940963 0.3752191

Prediction outside range(Temp) is not recommended, as it suffers from potential bad extrapolation effect.

---

Before I resort to non-parametric method, I also tried non-linear regression with regression splines and orthogonal polynomial basis, but they don't provide satisfying result. The major reason is that there is no penalty on the smoothness. As an example, I show some try with poly:

try1 <- lm(Disc ~ poly(Temp, degree = 3))
try2 <- lm(Disc ~ poly(Temp, degree = 4))
try3 <- lm(Disc ~ poly(Temp, degree = 5))

plot(Temp, Disc, ylim = c(-0.3,1.0))
x<- seq(min(Temp), max(Temp), length = 50)
newdat <- list(Temp = x)
lines(x, predict(try1, newdat), col = 2)
lines(x, predict(try2, newdat), col = 3)
lines(x, predict(try3, newdat), col = 4)

We can see that the fitted curve is artificial.

Answer 2

We can fit polynomials as follows, but it's going to overfit the data as we have higher degree:

m <- nls(Disc ~ a + b*Temp + c*Temp^2 + d*Temp^3 + e*Temp^4, start=list(a=0, b=1, c=1, d=1, e=1))
plot(Temp,Disc,pch=19)
lines(Temp,predict(m),lty=2,col="red",lwd=3)

m <- nls(Disc ~ a + b*Temp + c*Temp^2 + d*Temp^3 + e*Temp^4 + f*Temp^5, start=list(a=0, b=1, c=1, d=1, e=1, f=1))
lines(Temp,predict(m),lty=2,col="blue",lwd=3)
m <- nls(Disc ~ a + b*Temp + c*Temp^2 + d*Temp^3 + e*Temp^4 + f*Temp^5 + g*Temp^6, start=list(a=0, b=1, c=1, d=1, e=1, f=1, g=1))
lines(Temp,predict(m),lty=2,col="green",lwd=3)

m.poly <- lm(Disc ~ poly(Temp, degree = 15))
lines(Temp,predict(m),lty=2,col="yellow",lwd=3)

legend(x = "topleft", legend = c("Deg 4", "Deg 5", "Deg 6", "Deg 20"),
       col = c("red", "green", "blue", "yellow"),
       lty = 2)