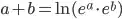Implementing addition using multiplication

Question

I've been familiar with the famous question of implementing multiplication using addition, or exponentiation using multiplication, using algorithms of looping or bit-shifting and adding shifted bit groups combos.

Now, I wondered if there is any way to implement addition using only higher level operations, such as multiplication specifically, or exponentiation, logarithm etc. (subtraction excluded)

Can this be achieved with some algorithm combining these operations (and possibly bitwise operators as assistants) or is addition a fundamental operation that serves as an axiom, so it can't be reproduced in other ways except for its definition?

Thanks.

I'm not a mathematician, but I'm not aware of any such thing. — duffymo, Sep 14 '16 at 13:02
Is it acceptable if one write a program without using add / subtract but use some data structure like set, map, vector, list, etc? — shole, Sep 15 '16 at 02:36
Voting to leave closed as not a practical programming problem. — ivan_pozdeev, Oct 19 '16 at 02:25

score 7 · Answer 1 · edited Sep 15 '16 at 14:24

7

Yes of course:

a + b = ln(exp(a) * exp(b))

Edit: Lifting my eyes above the practicality above to the more speculative, I would say that you should expect to be able to perform lower level operations through higher. As long as the higher level operation is built up by lower level operations, these should be able to perform at least what their building stones could. However probably not in an easy and straightforward way, see the comment below. A human can tell you that 1+1=2 but it would be much much cheaper and safer to ask a computer or an even simpler device.

edited Sep 15 '16 at 14:24

Uriel

15,579
6
25
46

answered Sep 14 '16 at 08:45

Mats Lind

914
7
19

4

Please note the risk of overflow and inaccurate result if used in real systems – Leon Sep 14 '16 at 08:49
What if we want to use operations that are actually implementable, can it still be done? – harold Sep 14 '16 at 10:17
1

Well, ln() and exp() are of course implementalbe as is ln(exp(a)*exp(b)), but if you mean "Implementable without using addition", then we are basically talking about performing addition without performing addition. That should be really hard. – Mats Lind Sep 14 '16 at 11:47
3

I meant implementable as in on a computer. `ln` and `exp` themselves only exist in mathematics, in practice only approximations can exist since otherwise the result has infinitely many bits and can never be produced. So I was hoping for something in finite rings/fields or else BigInt and the corresponding rationals. – harold Sep 14 '16 at 12:44

m69's been on strike for years · Answer 2 · 2016-09-15T02:21:01.147

2

Well, if you want to be pedantic about it, two numbers in binary representation can be added up using only the bitwise operators OR, XOR and AND, without strictly "adding" anything. For the sum a + b = c, the n-th bit can be calculated like this:

c_n = a_n XOR b_n XOR carry
carry = (a_n AND b_n) OR ((a_n XOR b_n) AND carry)

And you should of course avoid using n++ when iterating over the bits, and throw in a couple of multiplications for good measure:

int add(int a, int b) {
    int c = 0;
    char carry = 0;
    for (int mask = 1; mask; mask *= 2) {
        char an = a & mask ? 1 : 0;
        char bn = b & mask ? 1 : 0;
        c |= (an ^ bn ^ carry) * mask;
        carry = an & bn | (an ^ bn) & carry;
    }
    return c;
}

edited Sep 15 '16 at 02:21

answered Sep 14 '16 at 22:05

m69's been on strike for years

11,835
3
34
57

1

That's not quite pedantic enough. Please define "strictly adding." (As far as I can tell, what you describe with the bit-operations actually more closely resembles what the computer actually does when we hit `+`.) – גלעד ברקן Sep 14 '16 at 23:14
That's one headstrong interpretation of `Using Multiplication`/**only** _higher level operations, such as multiplication specifically, or_ [transcendentals]. – greybeard Sep 15 '16 at 08:26
1

@greybeard I took the words "some algorithm combining these operations (and possibly bitwise operators)" quite literally :-) – m69's been on strike for years Sep 15 '16 at 13:32
@UrielEli Well, `c |= (an ^ bn ^ carry) * mask` has a real multiplication, though you could write `if (an ^ bn ^ carry) c |= mask`. (You could also argue that the `|=` is actually a sum, that could be written as `+=`, and you'd have a point.) – m69's been on strike for years Sep 15 '16 at 20:26

Implementing addition using multiplication

2 Answers2