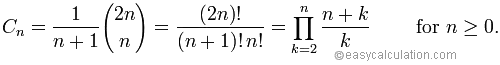0

I'm new to python (and programming in general), I was asked in my class to calculate Catalan numbers up to a billion but the program I wrote for it is not working as intended.

    from numpy import division 
    C=1
    n=0
    while C<=10000000000:
        print (C)
        C=(4*n+2)/(n+2)*C
        n=n+1

This is what it prints

1, 1, 2, 4, 8, 24, 72, 216, 648, 1944, 5832, 17496, 52488, 157464, 472392, 1417176, 4251528, 12754584, 38263752, 114791256, 344373768, 1033121304, 3099363912, 9298091736,

As you can see from my fourth iteration onwards, I get the wrong number and I don't understand why.

EDIT: The mathematical definition I used is not wrong! I know the Wiki has another definition but this one is not wrong. Co=1, Cn+1 = (4*n+2)/(n+2)*Cn

Guy Coder
  • 24,501
  • 8
  • 71
  • 136
Luis F Llano
  • 41
  • 11
  • 1
    What are Catalan numbers? What is the output you were expecting? – ffledgling Sep 09 '16 at 15:48
  • it is a series of numbers used in quantum mechanics and the theory of disordered systems. the answer I was expecting was: 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190 The formula I was given was Co=1, Cn+1=(4*n+2)/(n+2)*Cn – Luis F Llano Sep 09 '16 at 15:50
  • Please provide the actual specific definition of a Catalan number. – J Earls Sep 09 '16 at 15:52
  • The problem is because you're using integer division. Try a slight reordering of the terms: `C = ((4 * n + 2) * C) / (n + 2)` – Phylogenesis Sep 09 '16 at 15:54

5 Answers5

3
        C=(4*n+2)/(n+2)*C

This applies the calculation in the wrong order. Because you are using integer arithmetic, (4*n+2)/(n+2) loses information if you have not already factored in C. The correct calculation is:

        C=C*(4*n+2)/(n+2)
J Earls
  • 1,792
  • 8
  • 12
  • Thank you very much! that was what I was looking for. I'm very new to programming thank you for pointing out the explanation. – Luis F Llano Sep 09 '16 at 16:07
0

Try this:

from scipy.special import factorial

C = 1
n = 0
while C <= 10000000000:
    print(C)
    C = factorial(2*n, exact=True)/(factorial((n+1), exact=True)*factorial(n, exact=True))
    n = n + 1

It works for me :)

Kostas Belivanis
  • 397
  • 1
  • 5
  • 17
0

The problem

Your mathematical definition of Catalan numbers is incorrect when translated into code.

This is because of operator precedence in programming languages such as Python.

Multiplication and division both have the same precedence, so they are computed left to right. What happens is that the division operation (4*n+2)/(n+2) happens before the multiplication with C. When n is 2, 2*(2*n+2)/(n+2) becomes 10/4 which is 2 in integer arithmetic. 1*C which is 2 at this stage, gives 4 instead of giving the expected 5. Once a number in the series is incorrect, being computed iteratively is incorrect.

A possible work around

Here's the definition Catalan Numbers

enter image description here

Which means, the nth Catalan number is given by:

import operator as op

def ncr(n, r):
    r = min(r, n-r)
    if r == 0: return 1
    numer = reduce(op.mul, xrange(n, n-r, -1))
    denom = reduce(op.mul, xrange(1, r+1))
    return numer//denom


def catalan(n):
    return ncr(2*n, n)/(n+1)

This is not very efficient, but it is at least correct.

The right fix

To compute the series, you can do, using the recursive formula.

enter image description here

N=1000000 # limit
C=1
for i in xrange(0, N+1):
    print i,C
    C = (2*(2*i +1)*C)/(i+2)

For the first few, it looks like this:

0 1
1 1
2 2
3 5
4 14
5 42
6 132
7 429
8 1430
9 4862
10 16796
Community
  • 1
  • 1
ffledgling
  • 11,502
  • 8
  • 47
  • 69
  • There is a way to define one Catalan number in terms of the previous term shown on the Wikipedia page. – Phylogenesis Sep 09 '16 at 15:57
  • Yes, there is, and that is likely more efficient when computing the series, but I wanted to point out the formula for the *Nth* term as indicated in the definition. I'll add a piece of code for that as well. – ffledgling Sep 09 '16 at 15:58
0

This is solved using recursion:

def catalan(n):
    if n <=1 :
        return 1

    res = 0
    for i in range(n):
        res += catalan(i) * catalan(n-i-1)

    return res

for i in range(10000000000):
    print (catalan(i))

you can read more about Catalan numbers here or here

Daniel Kravetz Malabud
  • 797
  • 3
  • 12
0

Based on this expression for Catalan Numbers:

enter image description here

from math import factorial

C = 1
n = 0
while C <= 10000000000:
    print(C)
    C = (factorial(2 * n)) / (factorial(n + 1) * factorial(n))
    n = n + 1

Returns:

1
1.0
1.0
2.0
5.0
14.0
42.0
132.0
429.0
1430.0
4862.0
16796.0
58786.0
208012.0
742900.0
2674440.0
9694845.0
35357670.0
129644790.0
477638700.0
1767263190.0
6564120420.0
ode2k
  • 2,653
  • 13
  • 20