0

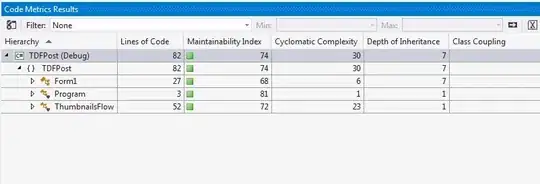
I was working with one dataset and found the curve to be sigmoidal. i have fitted the curve and got the equation A2+((A1-A2)/1+exp((x-x0)/dx)) where:

  • x0 : Mid point of the curve
  • dx : slope of the curve

I need to find the slope and midpoint in order to give generalized equation. any suggestions? enter image description here

pkt
  • 53
  • 12

2 Answers2

0

You should be able to simplify the modeling of the sigmoid with a function of the following form: Sigmoid (simple)

The source includes code in R showing how to fit your data to the sigmoid curve, which you can adapt to whatever language you're writing in. The source also notes the following form:

Sigmoid (General)

Which you can adapt the linked R code to solve for. The nice thing about the general functions here will be that you can solve for the derivative from them. Also, you should note that the midpoint of the sigmoid is just where the derivative of dx (or dx^2) is 0 (where it goes from neg to pos or vice versa).

Shawn
  • 409
  • 3
  • 12
  • Thankx Shawn! but my dataset has zero residual and fitting function giving nls single gradient error. – pkt Jul 24 '16 at 06:11
  • 1
    Assuming you're looking around, but have you seen the following links yet? http://r.789695.n4.nabble.com/Sigmoidal-fitting-td819800.html and https://rmazing.wordpress.com/2012/07/05/a-better-nls/ – Shawn Jul 24 '16 at 17:48
0

Assuming your equation is a misprint of A2+(A1-A2)/(1+exp((x-x0)/dx)) then your graph does not reflect zero residual, since in your graph the upper shoulder is sharper than the lower shoulder.

Likely the problem is your starting values. Try using the native R function SSfpl, as in nls(y ~ SSfpl(x,A2,A1,x0,dx))

Jerry W. Lewis
  • 1