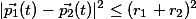I've been working on determining the time at which two objects would collide, if they would at all. I had referenced this thread which was very helpful: Circle-Circle Collision Prediction
(Oax + t*Dax - Obx - t*Dbx)^2 + (Oay + t*Day - Oby - t*Dby)^2 = (ra + rb)^2
I was able to solve that for t but now I'm wondering how I would best apply drag/friction to it.
If ball1 is traveling at a fixed rate of 9, and ball2 is traveling at 7... this works great. Problem is that if their velocities will decrease over time.. so if we're covering a lot of ground, ball1 will end up traveling at 4 and so the collision result could change.
For example: Ball1 is traveling down a slight slope, gaining speed. Ball2 is going straight and losing speed.
I'm assuming that the part of this formula needing adjustment would be the t*Dax, t*Dbx, t*Day, and t*Dby. These appear to be linear, right? So I would want to replace these with something representing my damping.
There would probably be multiple things determining my damping such as: surface friction and gravity.. or could reference easing equations such as Robert Penner's equations in this file http://gsgd.co.uk/sandbox/jquery/easing/jquery.easing.1.3.js
Thanks!
Edit:
Looked up some projectile motion formulas and was playing around with d = V₀t - ½ at² . Was wondering if combining that would be the trick, but not sure where/how it would be applied. I considered the following...
(O₁x + (t·D₁x - a₁t²) - O₂x - (t·D₂x + a₂t²))² + (O₁y + (t·D₁y - a₁t²) - O₂y - (t·D₂y + a₂t²))² = (r₁ + r₂)²
Update (thanks to the post by willywonkadailyblah)
After working with it a bit, here's a quick Javascript example of it working. You can find references to Vector classes and Quartic solvers online.
// p1 = c1 + (v1 * t) + 0.5 * a1 * (t ^ 2)
// p2 = c2 + (v2 * t) + 0.5 * a2 * (t ^ 2)
var p1c = new Vector(10, 50),
p1v = new Vector(10, -10),
p1a = new Vector( 5, 2),
p2c = new Vector( 50, 10),
p2v = new Vector(-10, 10),
p2a = new Vector( -9, 0),
r1 = r2 = 15,
p1, p2,
oc, ov, oa,
A, B, C, D, E,
q, r, s, t, u;
var quadraticAnswers = solveQuadratic(p1c, p1v, p2c, p2v, r1);
var quarticAnswers = solveQuartic( p1c, p1v, p1a, p2c, p2v, p2a, r1, r2 );
console.log( "Quartic", quarticAnswers );
console.log( "Quadratic", quadraticAnswers );
console.log( "Best Quartic", quarticAnswers.bestAnswer );
function solveQuartic(p1c, p1v, p1a, p2c, p2v, p2a, r1, r2) {
// delta p
oc = p1c.subtract(p2c);
// delta v
ov = p1v.subtract(p2v);
// delta a
oa = p1a.subtract(p2a);
//
A = oa.magnitude().pow(2).multiply(0.25);
B = ov.multiply(oa);
C = oc.multiply(oa).add( ov.magnitude().pow(2) )
D = ov.multiply(oc).multiply(2);
E = oc.magnitude().pow(2);
q = A.x + A.y;
r = B.x + B.y;
s = C.x + C.y;
t = D.x + D.y;
u = E.x + E.y - Math.pow(r1 + r2, 2); // hidden because of the issue with radius not adding up
// the quartic/cubic/quadratic solver
var ret = solveEquations(q, r, s, t, u);
if (oa.x + oa.y < 0) {
ret.bestAnswer = ret.x4 || ret.x3 || ret.x2 || ret.x1;
}
else {
ret.bestAnswer = ret.x2 || ret.x1 || ret.x4 || ret.x3;
}
return ret;
}
VectorJS works well with this, but you have to manually add a pow method. https://evanw.github.io/lightgl.js/docs/vector.html
Here's a quartic/cubic/quadratic solver for JS. You'll need to do a fair amount of modification on the source to get it to work with your app or to translate it into other languages. http://www.freewebs.com/brianjs/ultimateequationsolver.htm
I was going to post a C++, but figured this would be easy for a lot of people and many people use JS nowadays.