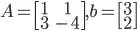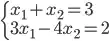What's wrong with my GMRES implementation?

Question

I'm trying to implement GMRES in Jupyter Notebook, which is (in case you don't know):

This is my code:

import numpy as np

def GMRes(A, b, x0, e, nmax_iter, restart=None):
    r = b - np.asarray(np.dot(A, x0)).reshape(-1)

    x = []
    q = [0] * (nmax_iter)

    x.append(r)

    q[0] = r / np.linalg.norm(r)

    h = np.zeros((nmax_iter + 1, nmax_iter))

    for k in range(nmax_iter):
        y = np.asarray(np.dot(A, q[k])).reshape(-1)

        for j in range(k):
            h[j, k] = np.dot(q[j], y)
            y = y - h[j, k] * q[j]
        h[k + 1, k] = np.linalg.norm(y)
        if (h[k + 1, k] != 0 and k != nmax_iter - 1):
            q[k + 1] = y / h[k + 1, k]

        b = np.zeros(nmax_iter + 1)
        b[0] = np.linalg.norm(r)

        result = np.linalg.lstsq(h, b)[0]

        x.append(np.dot(np.asarray(q).transpose(), result) + x0)

    return x

According to me it should be correct, but when I execute:

A = np.matrix('1 1; 3 -4')
b = np.array([3, 2])
x0 = np.array([1, 2])

e = 0
nmax_iter = 5

x = GMRes(A, b, x0, e, nmax_iter)

print(x)

Note: For now e is doing nothing.

I get this:

[array([0, 7]), array([ 1.,  2.]), array([ 1.35945946,  0.56216216]), array([ 1.73194463,  0.80759216]), array([ 2.01712479,  0.96133459]), array([ 2.01621042,  0.95180204])]

x[k] should be approaching to (32/7, -11/7), as this is the result, but instead it is approaching to (2, 1), what am I doing wrong?

What is the source of the pseudocode? Update: Numerical Analysis - Timothy Sauer — Thomas Wagenaar, Feb 24 '23 at 12:46

score 10 · Accepted Answer · answered Jun 22 '16 at 14:43

I think the algorithm is giving the correct result.

You are trying to solve Ax=b where:

$A = \begin{bmatrix} 1 & 1 \ 3 & -4 \end{bmatrix}, b = \begin{bmatrix} 3 \ 2 \end{bmatrix}$

If you try to find a solution by hand, the matrix operation you are trying to solve is equivalent to a system that can be solved using substitution.

$\begin{cases} x_1 + x_2 = 3 \ 3x_1-4x_2 = 2\end{cases}$

If you try to solve it you'll see that the solution is:

x_1=2,x_2=1

Which is the same solution your algorithm is giving.

You can double check this using the GMRES implementation already in scipy:

import scipy.sparse.linalg as spla
import numpy as np

A = np.matrix('1 1; 3 -4')
b = np.array([3, 2])
x0 = np.array([1, 2])
spla.gmres(A,b,x0)

Which outputs

array([ 2.,  1.])

I'm the most stupid person in the world, hours wasted because I solved incorrectly the equation xD... Thanks! — Patricio Sard, Jun 22 '16 at 17:43

score 5 · Answer 2 · answered Dec 11 '17 at 22:02

Note that this algorithm is converging to the correct result, but is doing so too slowly. The maximum number of GMRES iterations to converge should never exceed the dimension of the matrix A. If the dimension of the matrix A is n, then the (n+1)'th Arnoldi vector should be zero, e.g. we should be able to completely span the Krylov space with n Arnoldi vectors. I would just apply the following patch, and things should work as they should:

-    for k in range(nmax_iter):
+    for k in range(min(nmax_iter, A.shape[0])):
         y = np.asarray(np.dot(A, q[k])).reshape(-1)

-        for j in range(k):
+        for j in range(k + 1):

The solution vector sequence should then just be:

 [array([ 1.        ,  0.35294118]), array([ 2.,  1.])]

e.g. we converged in two iterations which we expect since n = 2.

What's wrong with my GMRES implementation?

2 Answers2