my original problem was the following:
I have a pulse-envelope in an array a (0-element = time 0, last element = time T).
I want to fourier spectrum of the pulse. So what I did was np.fft.fftshift(np.fft.fft(a)). All good.
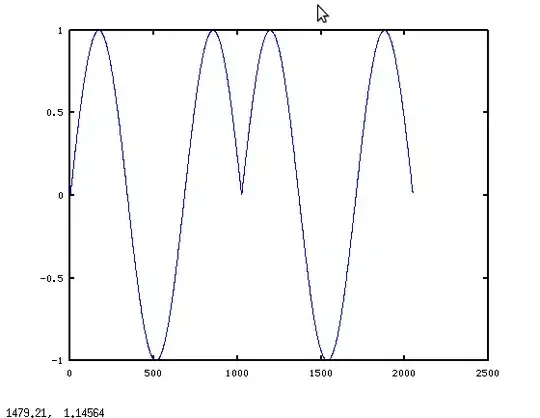
But then I was told to do a shift beforehand, too: np.fft.fftshift(np.fft.fft(np.fft.fftshift(a))). Then oscillations arised.
Now I wonder why one would do 2 shifts as shown above and why oscillations arise...
Here the example: I have the following code
x = np.arange(100)
a =np.sin(np.pi*x**2/1000)
a_fft = np.fft.fft(a)
a_fft_shift = np.fft.fftshift(a_fft)
a_shift = np.fft.fftshift(a)
a_shift_fft = np.fft.fft(a_shift)
a_shift_fft_shift = np.fft.fftshift(a_shift_fft)