Assignment Problem when jobs are available more than once

Question

I have a normal assignment problem, where I want to match workers to jobs. But there are several kinds of jobs, each with a set amount of positions. So for example I would need 10,000 builders, 5,000 welders etc. Each worker has of course the same preference for each position of the same kind of job.

My current approach is to use the Hungarian Algorithm and to just extend the matrix columns to account for that. So for example it would have 10,000 builder columns, 5,000 welder etc. Of course with O(n³) and a matrix that big, getting results may take a while.

Is there any variation of the Hungarian algorithm, or a different one, which uses the fact, that there can be multiple connections to one job node? Or should rather look into Monte Carlo or genetic search tree algorithms?

edit:

Formal description as Sascha proposed:

Set W for workers, J for jobs, weight function 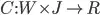for the preference, function 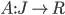for the amount of jobs available

So the function I want to minimize would be:

where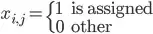

Constraints would be:

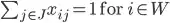
and

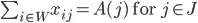
As asked by Yay295, it would be ok if it ran for a day or two on a normal consumer machine. There are 50k workers right now with 10 kinds of jobs and 50k jobs total. So the matrix is 50k x 50k (extended) in the case of the Hungarian algorithm I'm using right now, or 50k x 10 for LP with the additional constraint 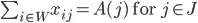, while and preference values in the matrix would go from 0-100.

Answer 1

This is actually called the Transportation Problem. The Transportation Problem is similar to the Assignment Problem in that they both have sources and destinations, but the Transportation Problem has two more values: each source has a supply, and each destination has a demand. The Assignment Problem is a simplification of the Transportation Problem in which the supply of each source and the demand of each destination is 1.

In your case, you have 50,000 sources (your workers) each with a supply of 1 (each worker can only work one job). You also have 10 destinations (the job types) each with some amount of demand (the number of openings for that type).

The Transportation Problem is traditionally solved with the Simplex Algorithm. I couldn't tell you how it works off the top of my head, but there is plenty of information available elsewhere online on how to do it. I would recommend these two videos: first, second.

 

Alternatively, the Transportation Problem can actually also be solved using the Hungarian Algorithm. The idea is to keep track of your supply and demand separately, and then use the Hungarian Algorithm (or any other algorithm for the Assignment Problem) to solve it as if the supply and demand were 1 (this can be incredibly fast when it's as lopsided as 50,000 sources to 10 destinations as in your case). Once you've solved it once, use the results to decrement the supply and demand of the assigned solution appropriately. Repeat until the sum of either supply or demand is zero.

However, none of this may be necessary. I wrote my own Assignment Problem solver in C++ a few years ago, and despite using 2.5GB of RAM, it can solve a 50,000 by 50,000 assignment problem in less than 5 seconds. The trick is to write your own. Before I wrote mine I had a look around at what was available online, and they were all pretty bad, often with obvious bugs. If you are going to write your own code for this though, it would be better to use the Simplex Algorithm as described in the videos I linked above. I don't know that one is faster than the other, but the Hungarian Algorithm wasn't made for the Transportation Problem.

 

ps: The same person who did the two lectures I linked above also did one on the Assignment Problem and the Hungarian Algorithm.