0

Perhaps this isn't a programming question but a math question. But here goes.

Imagine that you are making a roller coaster powered by a motor on the vehicle. The vehicles have a fixed force value that they can achieve using this motor. In a section of your roller coaster you want to traverse a half loop like this one from one of my favorite video games: Rollercoaster Tycoon!

A good old half loop from Rollercoaster Tycoon

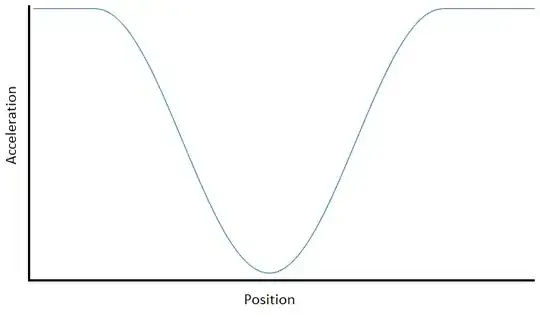
As you go around the half loop, you don't know what your speed will be or how long it will take you to go around it. However, you can figure out based on your engine acceleration, mass, and acceleration due to gravity what your maximum possible acceleration at any point along the half loop will be. Let's not muddle this discussion up with numbers, but instead assume that we've got the acceleration vs position curve available. It looks something like this:

enter image description here

I have successfully derived the formula for the velocity as a function of the acceleration vs position curve and the initial velocity. From the kinematic equation 

v^2 = 2*a*p

I can derive the velocity as a function of position. v = sqrt(2 * [integral of a=f(p) wrt position])

which in MATLAB I can get by doing:

v = sqrt(2.*abs(trapz(pos, acc)));

I actually am getting the velocity of every point along the track with the following code (acc and pos are arrays of acceleration vs position plotted above):

vel = 1;
newAcc = 0;
while ix <= length(acc)
    pa = acc(ix-1) + (acc(ix)-acc(ix-1))./2;
    newAP = (pos(ix)-pos(ix-1)).*pa; % This is more time efficient than trapz
    newAcc = newAcc + abs(2.*newAP);
    vel(ix) = sqrt(newAcc);
    ix = ix + 1;
end

Now I reach my dilemma. I have acceleration, velocity, and position, and now I need time. I think my math is correct. Since I have a/v/p it should just be as simple as choosing any of the kinematic equations involving time and rearranging it to get time (I want to get the time at every position along the track so I can plot a/v/p as functions of time).

This should mean I can pick from any of these:

1.  p_f = p_i + v_i*t + 1/2*a*t^2
2.  v_f = v_i + a*t
3.  p = (v_i + v_f)*t/2

Equation 1 is a quadratic. The other two look much simpler. Equation 2 looks promising. Let's try that.

t = (v_f - v_i)/a

Converting this to Matlab, I think it should be this:

time = 0;
while ix <= length(acc)
    pa = acc(ix-1) + (acc(ix)-acc(ix-1))./2;
    newAP = (pos(ix)-pos(ix-1)).*pa; % This is more time efficient than trapz
    newAcc = newAcc + abs(2.*newAP);
    vel(ix) = sqrt(newAcc);

    dt = (vel(ix)-vel(ix-1))./acc(ix);
    time(ix) = time(ix-1) + dt;
    ix = ix + 1;
end

But so far from my testing, this produces an incorrect result! I'm stumped on both the math and the algorithm. But I suppose this place is simply to answer the question about the algorithm. I can't see how my formula would be incorrect. Am I converting it in to Matlab incorrectly?

toshiomagic
  • 1,335
  • 1
  • 12
  • 39
  • I'm pretty sure that this is indeed not a programming question. I think your question would be better suited in the Physics section of Stack Exchange. How did you verify your result by the way? How do you know it's wrong? – tvo Jun 01 '16 at 21:35
  • I don't believe the physics or the programming are correct. I expect to see Seret-Frenet formulas for equations of motion along a curve. There should be vector quantities, since displacements, velocities and accelerations are all vectors. This is wrong from beginning to end. – duffymo Jun 01 '16 at 23:53
  • This is not wrong from beginning to end. I create a curve using constant time steps and my acceleration vs position curve. I match this curve to what I'm getting here. The position and velocity are correct. – toshiomagic Jun 03 '16 at 19:10

1 Answers1

0

The following code is the solution. I've been sitting on this for awhile, just forgot to answer the question.

while p < pf
    vel(i) = real(sqrt(vel(i-1).^2 + 2 .* ((acc(i)+acc(i-1))./2) .* (pos(i)-pos(i-1)) ));
    time(i) = time(i-1) + (pos(i)-pos(i-1)) ./ ( (vel(i)+vel(i-1))./2 );
    i = i + 1;
end

The time function comes from a rearrangement of

d = (vi+vf)*t/2

modified for an array of position values.

toshiomagic
  • 1,335
  • 1
  • 12
  • 39