4

I have been pondering about my homework question for a while. I welcome (and prefer) any suggestions or approach on how to attack this problem.

Basically, I have an array A of size N. We do not know the elements but we know they are distinct. The only thing that I have is a person who will take two indices (i,j) in N. This person will then tell me whether A[j] is < or > A[i]. I want to find the algorithm for finding the index of the 2nd smallest element by asking <= n + log n questions to this person.

denniss
  • 17,229
  • 26
  • 92
  • 141
  • So what have you done so far ? By now I'd have written a few small vaguely random arrays on paper, generated some i,j pairs and started to figure things out. – High Performance Mark Sep 15 '10 at 08:37
  • i was thinking of selecting a number randomly, and i would then partition the array into two parts, big and small. I realize that this would change the indexing of the array and now I am working on how to let the elements stay where they are... may be just move the indices around? – denniss Sep 15 '10 at 08:42
  • Can you modify the array? Or allocate another array and move elements from `A` to that array? – IVlad Sep 15 '10 at 10:37
  • Duplicate of http://stackoverflow.com/questions/3628718/ – sdcvvc Sep 16 '10 at 19:25
  • So similar to https://stackoverflow.com/a/65520791/11350682 – Shrm Dec 31 '20 at 12:15

7 Answers7

23

This answer describes how to find the second greatest element; finding the second smallest can be done analogously. For simplicity, we also assume that all numbers are different.

In order to find the greatest element, let us build a 'championship' tree: pair up the elements, decide which is greater (that one is the 'winner') then pair up the winners, decide which is greater, and so on, until you find the 'champion', which is the greatest element. This takes n steps. Now, the second greatest element must have been compared to the champion. (because only the champion could defeat it). log n elements have been compared to the champion, so from these, pick the greatest; this takes log n steps.

As an example, let us see how this works for the number tuple [6,4,3,5,2,1] . In the first round, pairs are (6,4), (3,5), (2,1). Winners are the greater elements in each pair, that is, 6,5,2. In the second round pairs are (6,5), 2. (2 has no pair here so it will get promoted to the next round automatically). Winners of the second round are 6 and 2, in the third round the only pair is (6,2), 6 is the winner. Now, by pairing up elements and choosing a winner we have built up a (rooted, binary) tree: 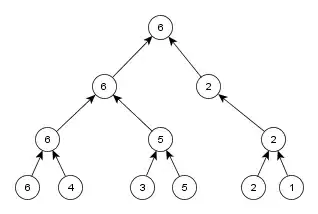alt text

This tree has the property that for a node x and its children y,z we have x>=y, x>=z, so we know that the greatest element is the one at the top (at the root). We also know that the second greatest element w did not make it to the top, so it has a parent in the tree. But its parent is greater than or equal to w, so at some level of the tree, one of the children of the greatest element is w. (In other words, the second greatest element could only be 'defeated' by the greatest element). So all we have to do is go back on the path the greatest element has taken and collect all direct children, we know the second largest is among them. In our case, these are the elements 2,5,4 . (In general, there are about log n of them, where log denotes base two logarithm, because the tree is about log n high.). From these elements we pick the largest with any method that takes log n steps, and we found the second largest.

All this may remind us to a championship, where numbers denote how 'good' each team is, hence the term 'championship tree'.

sandris
  • 1,363
  • 13
  • 27
  • `n + n/2 + n/4 + ... ` is not `n` steps, it's `2n`. – IVlad Sep 15 '10 at 10:04
  • @IVlad: in the first round, you start with n/2 comparisons, not n. – Henrik Sep 15 '10 at 10:17
  • yeah, well, not n but n-1 if we really want to speak strictly – sandris Sep 15 '10 at 10:21
  • @Henrik - how so? `1 2 3 4 5` - compare 1-2, 2-3, 3-4, 4-5, which is `n - 1` comparisons. @sandris - true, but still more than `n + log n` – IVlad Sep 15 '10 at 10:34
  • @IVlad: no, I believe he means 1-2 3-4 5-6 7-8, and then semi-finals and finals. n/2 + n/4 +... + 1 for n being a power of 2 is n-1. When n is not such a power, you can adjust things easily. – Eyal Schneider Sep 15 '10 at 10:41
  • @IVlad: Do you mean that log n denotes the natural logarithm of n rather than the base two logarithm? I don't think that's attainable. – sandris Sep 15 '10 at 11:26
  • is this really going to work? supose i have the following array [6,4,3,5,2,1]. On the lowest level of the tree I will have (6,4) (3,5) (2,1). THe second largest is 2 but when I get The min of each pair i will get (4,3) (2,1) => (3,1) and the second largest is 3? – denniss Sep 16 '10 at 20:55
  • @My previous response: getMax also won't do it for this. – denniss Sep 16 '10 at 21:01
  • @denniss: Sorry, there's some confusion: my answer aimed at finding the greatest element rather than the smallest as your question required. I edited the answer and added some clarification. – sandris Sep 17 '10 at 06:59
  • You can write lg instead of log to make it base 2. – technazi Oct 23 '16 at 00:24
2

First, find the smallest element. You can do this with n-1 comaparisons in such a way, that each element is compared to at most log(n) other elements. Now look which elements have been compared to the smallest element and find the smallest of those.

Henrik
  • 23,186
  • 6
  • 42
  • 92
1
unknown array = a[].
min1 = a[0].              first element.
min2 = 0.                 can equal anything

for(start at 0, until the end, grow by one):
    if(min1 > a[n]):
      min2 = min1.
      min1 = a[n].

return min2.
sabbibJAVA
  • 1,068
  • 1
  • 11
  • 17
  • 2
    complextity of only n+3 or maybe n+5 – sabbibJAVA Jul 28 '12 at 21:57
  • You should compare also with the second value for the case when `a[min2] < a[n] < a[min1]`. – didierc Jan 26 '13 at 02:17
  • no reason to do that, just making it more complicated and increasing the complexity. – sabbibJAVA Feb 09 '13 at 00:21
  • indeed, I didn't see it that way! So what would be the result of your algorithm on `a = [-5;-4;-3]`? Would it be `-4`? Or `0`? Hold on...Is `0` a part of `a` here? – didierc Feb 09 '13 at 02:12
  • This algorithm is incorrect. It depends upon the 2nd smallest element occurring before the smallest in the sequence. If you feed it input [1, 3, 2], it will answer 1, not the correct answer 2. – curveship Sep 19 '13 at 20:21
1

Legends

S Space Complexity T Time Complexity

I'm Arnab Dutta. I've a say...why not go for: 

1. maintain the elements as a MIN-HEAP array
                       [S = 0, 
                        T = O(n) if optimized <- ignore as its 1 time activity]
2. call deleteMin() 2 times 
                       [T <= h(tree_height) 
                                   - as internally deleteMin() calls shiftDown()]

So total T = O(h)

Any one having an explanation why this is not better that using

     a. Tournament or
     b. using MAX-HEAP

Note: Step 1 can be argued about the Space and Time complexity.

Arnab Dutta
  • 168
  • 11
0

Attacking such problems is often best done by "divide and conquer". I.e. try to simplify/divide the problem, solve the simpler problem(s), then see if it gave any insight which helps you solving the original question. If the simpler problem is still too hard, try to simplify it further, etc.

In this case, you could start by finding the smallest element from the array. How would you do that?

Péter Török
  • 114,404
  • 31
  • 268
  • 329
0

Look into sorting algorithms like merge sort, which has a worst case complexity of O(n log n). The "person" telling you if A[j] > A[i] is true or false is obviously a comparison function.

Merge sort works by recursively dividing your array into two smaller arrays half the size of the original array, then applying the merge sort algorithm to these arrays again. If you arrive at a final step of two arrays with only one element, you ask the person/comparison function to tell you how to sort these arrays/elements. From this step up, you begin to merge your sub-arrays back into your orginal, but now sorted array.

At the end, you can simply return the second element of the sorted array, this being the second smallest.

Jim Brissom
  • 31,821
  • 4
  • 39
  • 33
0
  1. Use 2 variables - varSmallest and var2ndSmallest
  2. Ask person to compare 1st and 2nd value in array - set index of smaller to varSmallest, and the other to var2ndSmallest
  3. Take the next index in sequence and name it varIndexToCheck
  4. Compare values of varIndexToCheck and of var2ndSmallest - if value of varIndexToCheck is larger than value of var2ndSmallest go to step 3
  5. Compare values of varIndexToCheck and of varSmallest - if value of varIndexToCheck is larger than value of varSmallest set var2ndSmallest = varIndexToCheck and go to step 3
  6. Else, set var2ndSmallest = varSmallest and varSmallest = varIndexToCheck and then go to step 3

Repeat until there are no more indexes. After that, resulting index is inside var2ndSmallest variable and it is O(n log n) complexity

Ivan Ferić
  • 4,725
  • 11
  • 37
  • 47
  • But this has a worst case complexity of about 2n; OP is looking for n + log n. – Henrik Sep 15 '10 at 09:27
  • 1
    It has O(n + log n) and I believe that the real question was in fact "Find the O(n + log n) algorithm that can find 2nd smallest element in array", but the OP wanted to create a story out of the question. – Ivan Ferić Sep 15 '10 at 09:49
  • 1
    OP wants n + log n; without O(). Note that O(n + log n) is the same as O(n). – Henrik Sep 15 '10 at 10:21