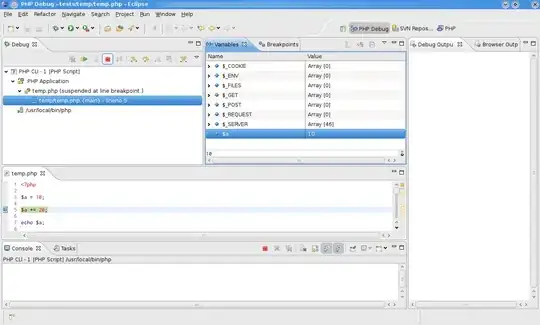
I need to calculate the angle between 3 points. I've done that using vectors, it looks like it's working, but sometimes I get NaN as a result. To calculate the angle I used the arcos(dot(v1,v2)/(length(v1)*length(v2))) formula. Here's the code:
private static double angleBetween(Point previous, Point center, Point next) {
Vector2D vCenter = new Vector2D(center.x, center.y );
Vector2D vPrev = new Vector2D(previous.x, previous.y );
Vector2D vNext = new Vector2D(next.x, next.y );
Vector2D a = vCenter.minus(vPrev);
Vector2D b = vCenter.minus(vNext);
double dot = Vector2D.dot(a, b);
double la = a.length();
double lb = b.length();
double l = la*lb;
double acos = Math.acos(dot/l);
double deg = Math.toDegrees(acos);
return deg;
}
Vector2D class:
public double length() {
return Math.sqrt(x * x + y * y);
};
public static double dot(Vector2D v1, Vector2D v2) {
return v1.x * v2.x + v1.y * v2.y;
};
public Vector2D minus(Vector2D v) {
return new Vector2D(x - v.x, y - v.y);
};
Debugging the program I've discovered why this happens. for example let be:
center = (127,356)
previous = (117,358)
next = (137,354)
//calculating the vectors
a = (-10,2) //center - prev
b = (10,-2) //center - next
dot = -10*10 + 2*-2 = 104
la = sqrt(-10*-10 + 2*2) = sqrt(104) = see attachment
lb = sqrt(10*10 + -2*-2) = sqrt(104) = see attachment
l = la * lb = see attachment
acos = NaN because dot/l>1 because I lost precision because of sqrt() which didn't give me the exact value therefore la*lb isn't 104.
now as far as I know double is the most precise number type in java. How can I solve this problem?
PS It may looks like a very rare situation, but I'm experiencing quite a lot of them, so I can't just ignore it.