4

Let's say I want to estimate the camera pose for a given image I and I have a set of measurements (e.g. 2D points ui and their associated 3D coordinates Pi) for which I want to minimize the error (e.g. the sum of squared reprojection errors).

My question is: How do I compute the uncertainty on my final pose estimate ?

To make my question more concrete, consider an image I from which I extracted 2D points ui and matched them with 3D points Pi. Denoting Tw the camera pose for this image, which I will be estimating, and piT the transformation mapping the 3D points to their projected 2D points. Here is a little drawing to clarify things:

enter image description here

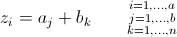
My objective statement is as follows: minimization objective statement

There exist several techniques to solve the corresponding non-linear least squares problem, consider I use the following (approximate pseudo-code for the Gauss-Newton algorithm):

enter image description here

I read in several places that JrT.Jr could be considered an estimate of the covariance matrix for the pose estimate. Here is a list of more accurate questions:

  1. Can anyone explain why this is the case and/or know of a scientific document explaining this in details ?
  2. Should I be using the value of Jr on the last iteration or should the successive JrT.Jr be somehow combined ?
  3. Some people say that this actually is an optimistic estimate of the uncertainty, so what would be a better way to estimate the uncertainty ?

Thanks a lot, any insight on this will be appreciated.

BConic
  • 8,750
  • 2
  • 29
  • 55

1 Answers1

6

The full mathematical argument is rather involved, but in a nutshell it goes like this:

  1. The outer product (Jt * J) of the Jacobian matrix of the reprojection error at the optimum times itself is an approximation of the Hessian matrix of least squares error. The approximation ignores terms of order three and higher in the Taylor expansion of the error function at the optimum. See here (pag 800-801) for proof.
  2. The inverse of the Hessian matrix is an approximation of the covariance matrix of the reprojection errors in a neighborhood of the optimal values of the parameters, under a local linear approximation of parameters-to-errors transformation (pag 814 above ref).

I do not know where the "optimistic" comment comes from. The main assumption underlying the approximation is that the behavior of the cost function (the reproj. error) in a small neighborhood of the optimum is approximately quadratic.

Francesco Callari
  • 11,300
  • 2
  • 25
  • 40
  • Thank you for your answer. So if I understand correctly, using JT.J as an estimate of the uncertainty is only valid when estimating the pose via minimization of the reprojection error? Or is the same argument valid for other cost functions as well? – BConic Apr 15 '16 at 05:05
  • 1
    Mathematically, Jt*J is just an approximation of the Hessian matrix of a nonlinear multidimensional least squares error near an optimum. That its inverse is an approximation of the covariance matrix of the error function's parameters is a separate (and much more involved) mathematical statement. I suggest you look up a good reference on data modeling and (nonlinear) least squares. In the computer vision arena you are interested in, a good start would be Triggs et al long report on bundle adjustment, see https://lear.inrialpes.fr/pubs/2000/TMHF00/Triggs-va99.pdf – Francesco Callari Apr 15 '16 at 13:09
  • You are welcome. BTW, I now think that the "optimistic" comment stems from confusing an estimation of the confidence intervals with assuming a Gaussian distribution of the residuals. This is a common misconception. – Francesco Callari Apr 15 '16 at 14:11
  • Could you clarify what you mean by that? I don't see the link between the "optimistic" comment and neither the estimation of confidence intervals nor the assumption of gaussian residuals. – BConic Apr 15 '16 at 14:40
  • 1
    If the cost function is exactly quadratic, then the Jt*J estimation is exact. Under the same assumption, the input->error transformation is linear. So the error bars predicted this way ignore, in a sense, the nonlinear part of said transformation. Under this assumption, the error bars are just that, estimations of variance. A common error is to assume that the residuals are (in addition to i.i.d.) also Gaussian, i.e. that the tails beyond those error bars are much less fat than in practice. Of course I did not mean to imply that you were operating under the same misconception. – Francesco Callari Apr 15 '16 at 15:52
  • Let us [continue this discussion in chat](http://chat.stackoverflow.com/rooms/109274/discussion-between-francesco-callari-and-aldurdisciple). – Francesco Callari Apr 15 '16 at 16:52
  • @FrancescoCallari I'm also interested in a mathematical explanation of the phenomenon, but the link you provided in the answer does no longer work: could you please leave a reference for the material? Thank you very much! – Lilla Jan 24 '21 at 20:32
  • 1
    @Leonardo it fell victim to the flashocalypse. Fixed, thanks. – Francesco Callari Jan 25 '21 at 23:41