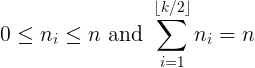"Data Structures and Network Algorithms" by Tarjan states the heapify function in leftiest heaps as following:
heap function heapify (list q);
do |q| ≥ 2 → := q[3..] & meld (q(1), q(2)) od;
return if q = [ ] → null | q != [ ] → q(1) fi
end heapify;
q is being the queue of heaps we would like to heapify together. meld(h1, h2) is being a function for merging two heaps and restoring the heap property. meld(h1, h2) is having the complexity O(logn), where n is the total number of nodes in both heaps. This makes the complexity for one pass through the queue as following:
which is plausible. What I do not get is the time for the entire heapify as it is:
k here is the number of original heaps and n the total number of items they contain. There are also two constrains mentioned beforehand:
Can somebody help me understand how the Eq. 2 is derived? (how one interprets the left expression of the equality in Eq. 2)