Boolean expression in SOP

Question

I'm new to boolean expressions.

I've been given the task to simplify F(w,x,y,z) = xy’ + x’z’ + wxz + wx’y by using K map.

I've done it and the result is wx’+w’y’+xyz.

Now I have to "Write it in a standard SOP form. You need to provide the steps through which you get the standard SOP".

And i have no idea how to do it. I thought result after k map is sop.

Not sure why but perhaps the intent is to have you write the 10 terms out in long form?? — shawnt00, Feb 05 '16 at 16:02

score 0 · Accepted Answer · answered Feb 05 '16 at 16:02

0

Yes, you already have it in SOP form. But the second question is about Standard (aka canonical) SOP form. That's much simpler to find than having to use K-maps (but it's often long), it's just the sum of minterms.

answered Feb 05 '16 at 16:02

harold

61,398
6
86
164

Could you briefly explain how can get this canonical SOP form? – Dominik Banialis Feb 05 '16 at 16:04
@DominikBanialis you know what minterms are, right? Just get them any way you like. Since you already have a short SOP here, you can make copies of every term for every combination of its "don't-care"'s, for example `xyz` -> `wxyz + w'xyz` – harold Feb 05 '16 at 16:08
Minterms are 0 s in Ttable whenever Output is T right? and maxterms ar 1s. And i should start from first expresion xy’ + x’z’ + wxz + wx’y. My result is going to be same as K map result? – Dominik Banialis Feb 05 '16 at 16:17
1

@DominikBanialis it won't be the same as the K map result (it might be, in some cases, but not now) because `xy'` is not a valid minterm (it doesn't mention all variables) and so on – harold Feb 05 '16 at 16:21

score 0 · Answer 2 · answered Jul 11 '16 at 10:02

I think your solution does not cover all ones. These Karnaugh maps show the original expression, the simplified version (minimal SOP) and the canonical SOP, where every product contains all literals (all given variables or their negation).

The original expression is

F(w,x,y,z) = x·¬y + ¬x·¬z + w·x·z + w·¬x·y

– there are two fours and two pairs circled in the corresponding (first one) K-map.

The original expression simplified using K-map (shown in the second one):

F(w,x,y,z) = x·¬y + ¬x·¬z + w·y·z

is different than yours, but you can check for example with wolframalpha online tool, that it is the simplified original expression.

It is also the minimal DNF, but not a sum of minterms (where the output is equal to 1), because there are not all variables in every product of the sum.

The third K-map shows ten minterms circled. They form the canonical DNF:

F(w,x,y,z) = m0 + m2 + m4 + m5 + m8 + m10 + m11 + m12 + m13 + m15 =
           = ¬w·¬x·¬y·¬z + ¬w·¬x·y·¬z + ¬w·x·¬y·¬z + ¬w·x·¬y·z + w·¬x·¬y·¬z 
             + w·¬x·y·¬z + w·¬x·y·z + w·x·¬y·¬z + w·x·¬y·z + w·x·y·z

I checked your simplified expression, but there are not all ones covered (even if there were some useful do not care states (marked X)). Maybe you made a typo. Or could there be a typo in the original expression?

Sandipan Dey · Answer 3 · 2021-12-02T23:21:43.713

We can implement the K-Map algorithm in python for 4 variables, as shown below. The function accepts the Boolean function in SOP (sum of products) form and the names of the variables and returns a simplified reduced representation. Basically you need to create rectangular groups containing total terms in power of two like 8, 4, 2 and try to cover as many elements as you can in one group (we need to cover all the ones).

For example, the function can be represented F(w,x,y,z) = xy’ + x’z’ + wxz + wx’y in SOP form as f(w,x,y,z)=∑(0,2,4,5,8,10,11,12,13,15), as can be seen from the below table:

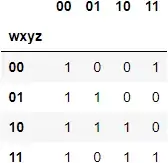
As can be seen from the output of the next code snippet, the program outputs the simplified form x¬y + ¬x¬z + wyz, where negation of a boolean variable x is represented as ¬x in the code.

from collections import defaultdict
from itertools import permutations, product
    
def kv_map(sop, vars):
    
    sop = set(sop)
    not_covered = sop.copy()
    sop_covered = set([])
    
    mts = [] # minterms
    
    # check for minterms with 1 variable
    all_3 = [''.join(x) for x in product('01', repeat=3)]
    for i in range(4):
        for v_i in [0,1]:
                if len(not_covered) == 0: continue
                mt = ('' if v_i else '¬') + vars[i]
                s = [x[:i]+str(v_i)+x[i:] for x in all_3]
                sop1 = set(map(lambda x: int(x,2), s))
                if len(sop1 & sop) == 8 and len(sop_covered & sop1) < 8: # if not already covered
                    mts.append(mt)
                    sop_covered |= sop1
                    not_covered = not_covered - sop1
        if len(not_covered) == 0:
           return mts
    
    # check for minterms with 2 variables
    all_2 = [''.join(x) for x in product('01', repeat=2)]
    for i in range(4):
        for j in range(i+1, 4):
            for v_i in [0,1]:
                for v_j in [0,1]:
                    if len(not_covered) == 0: continue
                    mt = ('' if v_i else '¬') + vars[i] + ('' if v_j else '¬') + vars[j]
                    s = [x[:i]+str(v_i)+x[i:] for x in all_2]
                    s = [x[:j]+str(v_j)+x[j:] for x in s]
                    sop1 = set(map(lambda x: int(x,2), s))
                    if len(sop1 & sop) == 4 and len(sop_covered & sop1) < 4: # if not already covered
                        mts.append(mt)
                        sop_covered |= sop1
                        not_covered = not_covered - sop1
    if len(not_covered) == 0:
        return mts

    # check for minterms with 3 variables similarly (code omitted)
    # ... ... ...
    
    return mts
    
mts = kv_map([0,2,4,5,8,10,11,12,13,15], ['w', 'x', 'y', 'z'])
mts
# ['x¬y', '¬x¬z', 'wyz']

The following animation shows how the above code (greedily) simplifies the Boolean function given in SOP form (the basic goal is to cover all the 1s with minimum number of power-2 blocks). Since the algorithm is greedy it may get stuck to some local minimum, that we need to be careful about.

Boolean expression in SOP

3 Answers3