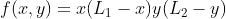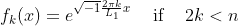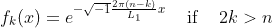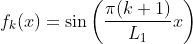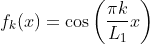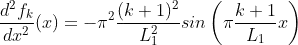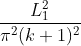fftw3 for poisson with dirichlet boundary condition for all side of computational domain

Question

I am trying to solve Poison equation with Dirichlet boundary condition for four sides of computational domain. As known that I should use FFTW_RODFT00 to satisfy the condition. However, the result is not correct.Could you please help me?

#include <stdio.h>
#include <math.h>
#include <cmath>
#include <fftw3.h>
#include <iostream>
#include <vector>

using namespace std;
int main() {

int N1=100;
int N2=100;

double pi = 3.141592653589793;
double L1  = 2.0;
double dx = L1/(double)(N1-1);
double L2= 2.0;
double dy=L2/(double)(N2-1);

double invL1s=1.0/(L1*L1);
double invL2s=1.0/(L2*L2);

std::vector<double> in1(N1*N2,0.0);
std::vector<double> in2(N1*N2,0.0);
std::vector<double> out1(N1*N2,0.0);
std::vector<double> out2(N1*N2,0.0);
std::vector<double> X(N1,0.0);
std::vector<double> Y(N2,0.0);


fftw_plan p, q;
int i,j;
p = fftw_plan_r2r_2d(N1,N2, in1.data(), out1.data(), FFTW_RODFT00, FFTW_RODFT00, FFTW_EXHAUSTIVE);
q = fftw_plan_r2r_2d(N1,N2, in2.data(), out2.data(), FFTW_RODFT00, FFTW_RODFT00, FFTW_EXHAUSTIVE);

int l=-1;
for(i = 0;i <N1;i++){
    X[i] =-1.0+(double)i*dx ;           
    for(j = 0;j<N2;j++){
        l=l+1;
        Y[j] =-1.0+ (double)j*dy ;
        in1[l]= sin(pi*X[i]) + sin(pi*Y[j]) ; // row major ordering
    }
}

fftw_execute(p);

l=-1;
for ( i = 0; i < N1; i++){   // f = g / ( kx² + ky² )  
    for( j = 0; j < N2; j++){
            l=l+1;
        double fact=0;
        in2[l]=0;

        if(2*i<N1){
            fact=((double)i*i)*invL1s;;
        }else{
            fact=((double)(N1-i)*(N1-i))*invL1s;
        }
        if(2*j<N2){
            fact+=((double)j*j)*invL2s;
        }else{
            fact+=((double)(N2-j)*(N2-j))*invL2s;
        }
        if(fact!=0){
            in2[l] = out1[l]/fact;
        }else{
            in2[l] = 0.0;
        }
    }
}

fftw_execute(q);
l=-1;
double erl1 = 0.;
for ( i = 0; i < N1; i++) {
    for( j = 0; j < N2; j++){
        l=l+1;

        erl1 +=1.0/pi/pi*fabs( in1[l]-  0.25*out2[l]/((double)(N1-1))/((double)(N2-1))); 
        printf("%3d %10.5f %10.5f\n", l, in1[l],  0.25*out2[l]/((double)(N1-1))/((double)(N2-1)));

    }
}

cout<<"error=" <<erl1 <<endl ;  
fftw_destroy_plan(p); fftw_destroy_plan(q); fftw_cleanup();

return 0;

}

Answer 1

I recognize a trick I provided you in Poisson equation using FFTW with rectanguar domain and the code I provided in my answer to Confusion testing fftw3 - poisson equation 2d test , which was adapted from the code of the asker @Charles_P ! Please consider adding links to these url in future questions !

The answer to Confusion testing fftw3 - poisson equation 2d test was devoted to the case of periodic boundary conditions. So here are a few modifications to solve the case of Dirichlet boundary conditions.

The fftw_plan_r2r_2d(N1,N2, in1.data(), out1.data(), FFTW_RODFT00, FFTW_RODFT00,FFTW_EXHAUSTIVE) corresponds to a type I discrete sine transform as defined by the FFTW library:

It's meaning is well described in https://en.wikipedia.org/wiki/Discrete_sine_transform . If the size of the FFTW array is N1=4 and its values [a,b,c,d], the full array including boundaries is [0,a,b,c,d,0]. Hence the spatial step is:

And the frequencies f_k of the type I DST are:

The inverse of the type I DST is the type I DST, except for a scale factor (see http://www.fftw.org/doc/1d-Real_002dodd-DFTs-_0028DSTs_0029.html#g_t1d-Real_002dodd-DFTs-_0028DSTs_0029), here 4.(N1+1).(N2+1).

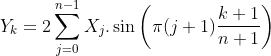
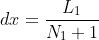
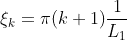
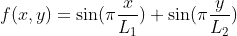Lastly, the test case must be adapted to the case of Dirichlet boundary conditions. Indeed, on the box of size L1,L2 the function does not respect the Diriclet boundary conditions. Indeed, even if the source term is the same, the solution satisfying periodic boundary conditions can be different from the solution satifying the Dirichelt boundary conditions. Instead, two source terms can be tested:

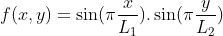• The source term corresponds to a single frequency of the DST.

• The source term is directly derived from the solution

Finally, here is a code solving the 2D Poisson equation using the type I DST of the FFTW library:

#include <stdio.h>
#include <math.h>
#include <cmath>
#include <fftw3.h>
#include <iostream>
#include <vector>

using namespace std;
int main() {

    int N1=100;
    int N2=200;

    double pi = 3.141592653589793;
    double L1  = 1.0;
    double dx = L1/(double)(N1+1);//+ instead of -1
    double L2= 5.0;
    double dy=L2/(double)(N2+1);

    double invL1s=1.0/(L1*L1);
    double invL2s=1.0/(L2*L2);

    std::vector<double> in1(N1*N2,0.0);
    std::vector<double> in2(N1*N2,0.0);
    std::vector<double> out1(N1*N2,0.0);
    std::vector<double> out2(N1*N2,0.0);
    std::vector<double> X(N1,0.0);
    std::vector<double> Y(N2,0.0);


    fftw_plan p, q;
    int i,j;
    p = fftw_plan_r2r_2d(N1,N2, in1.data(), out1.data(), FFTW_RODFT00, FFTW_RODFT00, FFTW_EXHAUSTIVE);
    q = fftw_plan_r2r_2d(N1,N2, in2.data(), out2.data(), FFTW_RODFT00, FFTW_RODFT00, FFTW_EXHAUSTIVE);

    int l=0;

    for(i = 0;i <N1;i++){
        for(j = 0;j<N2;j++){
            X[i] =dx+(double)i*dx ;      
            Y[j] =dy+ (double)j*dy ;
            //in1[l]= sin(pi*X[i])*sin(pi*Y[j]) ; // row major ordering
            in1[l]=2*Y[j]*(L2-Y[j])+2*X[i]*(L1-X[i]);
            l=l+1;
        }
    }

    fftw_execute(p);

    l=-1;
    for ( i = 0; i < N1; i++){   // f = g / ( kx² + ky² )  
        for( j = 0; j < N2; j++){

            l=l+1;
            double fact=0;

            fact=pi*pi*((double)(i+1)*(i+1))*invL1s;

            fact+=pi*pi*((double)(j+1)*(j+1))*invL2s;

            in2[l] = out1[l]/fact;

        }
    }

    fftw_execute(q);
    l=-1;
    double erl1 = 0.;
    for ( i = 0; i < N1; i++) {
        for( j = 0; j < N2; j++){
            l=l+1;
            X[i] =dx+(double)i*dx ;      
            Y[j] =dy+ (double)j*dy ;
            //double res=0.5/pi/pi*in1[l];
            double res=X[i]*(L1-X[i])*Y[j]*(L2-Y[j]);
            erl1 +=pow(fabs(res-  0.25*out2[l]/((double)(N1+1))/((double)(N2+1))),2); 
            printf("%3d %10.5g %10.5g\n", l, res,  0.25*out2[l]/((double)(N1+1))/((double)(N2+1)));

        }
    }
    erl1=erl1/((double)N1*N2);
    cout<<"error=" <<sqrt(erl1) <<endl ;  
    fftw_destroy_plan(p); fftw_destroy_plan(q); fftw_cleanup();

    return 0;
}

It is compiled by g++ main.cpp -o main -lfftw3 -Wall.

EDIT : How to compute the response to each frequency ?

The idea of FFT-based is to represent the solution as a linear combination of functions:

• In the case of periodic boundary conditions, the FFT is used. The base functions are:

• In the case of Dirichlet Boundary conditions, the type-I DST is used. The base functions, being 0 at x=0 and x=L1, are:

  

• In the case of Neumann boundary conditions, the type-I DCT is used. The base functions are:

  

Their derivatives are null at x=0 and x=L1.

Let's compute the second derivative of the componant f_k of the type-I DST:

Hence, the componant k of the DST of the solution corresponds to the componant k of the DST of the source term, scaled by a factor