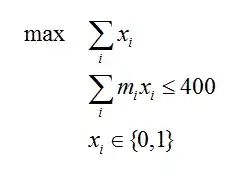Assign weights in lpSolveAPI to prioritise variables

Question

I am trying to set up a linear programming solution using lpSolveAPI and R to solve a scheduling problem. Below is a small sample of the data; the minutes required for each session id, and their 'preferred' order/weight.

id <- 1:100
min <- sample(0:500, 100)
weight <- (1:100)/sum(1:100)
data <- data.frame(id, min, weight)

What I want to do is arrange/schedule these session IDs so that there are maximum number sessions in a day, preferably by their weight and each day is capped by a total of 400 minutes.

This is how I have set it up currently in R:

require(lpSolveAPI)

#Set up matrix to hold results; each row represents day
r <- 5
c <- 10
row <- 1

results <- matrix(0, nrow = r, ncol = c)
rownames(results) <- format(seq(Sys.Date(), by = "days", length.out = r), "%Y-%m-%d")

for (i in 1:r){
    for(j in 1:c){  
        lp <- make.lp(0, nrow(data)) 
        set.type(lp, 1:nrow(data), "binary")
        set.objfn(lp, rep(1, nrow(data)))
        lp.control(lp, sense = "max")
        add.constraint(lp, data$min, "<=", 400)
        set.branch.weights(lp, data$weight)

        solve(lp)
        a <- get.variables(lp)*data$id
        b <- a[a!=0]

        tryCatch(results[row, 1:length(b)] <- b, error = function(x) 0)

        if(dim(data[!data$id == a,])[1] > 0) {
            data <- data[!data$id== a,]
            row <- row + 1
        }
        break

    }
}

sum(results > 0)    

barplot(results) #View of scheduled IDs

A quick look at the results matrix tells me that while the setup works to maximise number of sessions so that the total minutes in a day are close to 400 as possible, the setup doesn't follow the weights given. I expect my results matrix to be filled with increasing session IDs.

I have tried assigning different weights, weights in reverse order etc. but for some reason my setup doesn't seem to enforce "set.branch.weights".

I have read the documentation for "set.branch.weights" from lpSolveAPI but I think I am doing something wrong here.

Example - Data:

   id   min weight
    1   67  1
    2   72  2
    3   36  3
    4   91  4
    5   80  5
    6   44  6
    7   76  7
    8   58  8
    9   84  9
    10  96  10
    11  21  11
    12  1   12
    13  41  13
    14  66  14
    15  89  15
    16  62  16
    17  11  17
    18  42  18
    19  68  19
    20  25  20
    21  44  21
    22  90  22
    23  4   23
    24  33  24
    25  31  25

Should be

    Day 1   67  72  36  91  80  44  76          
    Day 2   58  84  96  21  1   41  66  89      
    Day 3   62  11  42  68  25  44  90  4   33  31

Each day has a cumulative sum of <= 480m.

I suspect branch weights (usually known as branching priority) is just to increase performance. It is not meant to generate structural different solutions. — Erwin Kalvelagen, Jan 08 '16 at 09:41
@ErwinKalvelagen That would make a lot of sense since (after posting this question) I decided to comment out the set.branch.weights and I still got the same results. Any idea otherwise how I can set weights to a linear programming solution in R? Cheers — sactyr, Jan 09 '16 at 07:50
You can do this through the objective. Any time you prefer one solution above another you should make sure the objective values for those two solutions reflect that. — Erwin Kalvelagen, Jan 09 '16 at 09:54
@ErwinKalvelagen Could you please tell me how can I change my objective function to include the weights, especially since this is a binary type? Will be much appreciated! — sactyr, Jan 09 '16 at 10:37
You use objective coefficients equal to 1. You could try something like 1+0.01*weight. I.e. counting is most important; weights are less important. — Erwin Kalvelagen, Jan 10 '16 at 00:16
@ErwinKalvelagen Thank you for that, I tried that but it doesn't seem to rank it the way I want it to. — sactyr, Jan 13 '16 at 22:31
It will choose x's with more weight. I'll put that in an answer to I have more space. — Erwin Kalvelagen, Jan 14 '16 at 05:22

score 1 · Accepted Answer · answered Jan 18 '16 at 12:07

My simple minded approach:

df = read.table(header=T,text="
 id   min weight
  1   67  1
  2   72  2
  3   36  3
  4   91  4
  5   80  5
  6   44  6
  7   76  7
  8   58  8
  9   84  9
  10  96  10
  11  21  11
  12  1   12
  13  41  13
  14  66  14
  15  89  15
  16  62  16
  17  11  17
  18  42  18
  19  68  19
  20  25  20
  21  44  21
  22  90  22
  23  4   23
  24  33  24
  25  31  25")
# assume sorted by weight 

daynr = 1
daymax = 480
dayusd = 0
for (i in 1:nrow(df))
{
  v = df$min[i]
  dayusd = dayusd + v
  if (dayusd>daymax)
  {
    daynr = daynr + 1
    dayusd = v
  }
  df$day[[i]] = daynr
}

This will give:

 > df
    id min weight day
 1   1  67      1   1
 2   2  72      2   1
 3   3  36      3   1
 4   4  91      4   1
 5   5  80      5   1
 6   6  44      6   1
 7   7  76      7   1
 8   8  58      8   2
 9   9  84      9   2
 10 10  96     10   2
 11 11  21     11   2
 12 12   1     12   2
 13 13  41     13   2
 14 14  66     14   2
 15 15  89     15   2
 16 16  62     16   3
 17 17  11     17   3
 18 18  42     18   3
 19 19  68     19   3
 20 20  25     20   3
 21 21  44     21   3
 22 22  90     22   3
 23 23   4     23   3
 24 24  33     24   3
 25 25  31     25   3
 >

Thank you! Yes it's off topic from the initial linear programming solution but the weights/ranking are important for me as this is a scheduling problem. A big thank you! — sactyr, Jan 18 '16 at 23:38

score 0 · Answer 2 · answered Jan 14 '16 at 05:37

0

I will concentrate on the first solve. We basically solve a knapsack problem (objective + one constraint):

When I run this model as is I get:

> solve(lp)
[1] 0
> x <- get.variables(lp)
> weightx <- data$weight * x
> sum(x)
[1] 14
> sum(weightx)
[1] 0.5952381

Now when I change the objective to

I get:

> solve(lp)
[1] 0
> x <- get.variables(lp)
> weightx <- data$weight * x
> sum(x)
[1] 14
> sum(weightx)
[1] 0.7428571

I.e. the count stayed at 14, but the weight improved.

answered Jan 14 '16 at 05:37

Erwin Kalvelagen

15,677
2
14
39

Hey, there is an improvement but I can't for some reason test it if I have more than 300 records - R just hangs. The other thing is I am looking for a solution that follows the weights strictly. I have added an example in the OP – sactyr Jan 15 '16 at 05:22
If you really want to fill the days purely in order of the weight there is no optimization left to do. Just start filling assigning items until you hit 480. Then move to the next day. No solver needed for this. – Erwin Kalvelagen Jan 15 '16 at 07:38
Yea that's what I am thinking now, unfortunately with my limited R I am trying to write a loop that will fill a matrix with the results. I am sure row cumsum <= 480 is involved. Any leads is appreciated, cheers – sactyr Jan 18 '16 at 02:59
No longer on-topic but I added a second answer for extra bonus points – Erwin Kalvelagen Jan 18 '16 at 12:08

Assign weights in lpSolveAPI to prioritise variables

2 Answers2