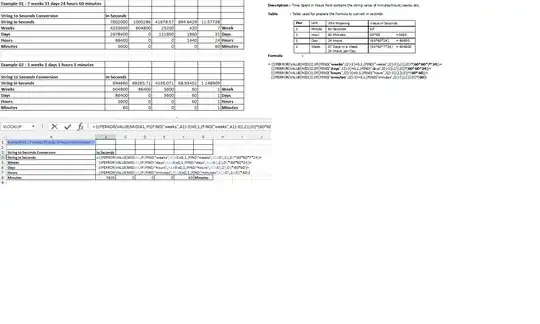
I'm using Pulp to solve a linear program (also getting the same result with scipy). So something wrong with my linear program formulation, or I don't know some tricky details on how simplex algorithm works.
Here is objective function for minimisation, notice that multiplier for x2 is 0, so I don't expect x1 or x2 to have any value except 0, because x3 doesn't have max constraint and -1 * x3 is able to provide more value for minimisation:
System of linear equations:
As a solution I'm getting x2 = 20 even if its multiplier in objective function is 0.
If in objective function I set -2 * x3, then it works just fine.