Image Processing - Using Radon Transform for Pattern Recognition in MATLAB

Question

I am attempting to extract the Radon Signature in order to recognize patterns of clothing (striped,plaid, irregular and patternless) as done in 1.

Algorithm to be implemented :

 1. Use sobel operator to compute the gradient map as f(x,y).
 2. Perform Radon transform based on maximum disk area.
 3. Compute the variance of r under all theta directions.
 4. Employ L2-norm to normalize the feature vector.
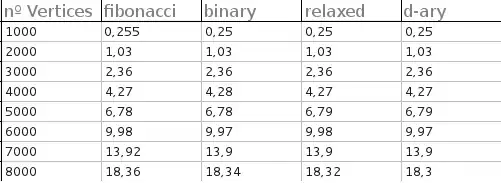
 5. Plot Radon Signature as a bar chart of var(r) for all theta values.

I have done the following :

img = imread('plaid.jpg');
grey = rgb2gray(img);
img2 = edge(grey, 'sobel');
vararray=zeros(1,size(theta,2));
theta = -89:90;
for j = 1: size(theta,2)
     [R3,xp3] = radon (img2,theta(j));
     vararray(j) = var(R3);
end
vararray = vararray/norm(vararray);
figure(1), bar(theta,vararray),title('Radon Signature');

I believe that my error lies in the first 2 steps. I am unsure how to perform Radon only on the maximum disk area.

My results are shown on the right, while from the article (referenced below) is shown on the left.

However, my results should at least show 2 distinct peaks as shown in the acticle's results, but they do not.

Any assistance is appreciated.

Source of Algorithm : "Assistive Clothing Pattern Recognition for Visually Impaired People" by Xiaodong Yang, Student Member, IEEE, Shuai Yuan, and YingLi Tian, Senior Member, IEEE

That figure from the article seems more of a doodle and less of an actual scientific figure. Are you sure it is to be taken seriously? Are you sure the theta range is the same? — Andras Deak -- Слава Україні, Dec 22 '15 at 19:22
The main thing to be taken from the graph of the article is the 2 dominant peaks. This should also be present in my results but it is not. I believe my error lies in the first algorithm step 1 but I am unsure how to do this in matlab — User404, Dec 22 '15 at 19:46
I can't help with the image-processing stuff, but you should pre-allocate vararray with `vararray=zeros(1,size(theta,2));` before the loop and use `vararray(j)` inside the loop, for speed. — Andras Deak -- Слава Україні, Dec 22 '15 at 20:03
Oh, and don't you mean `R3` instead of `var(R3)` in your above code, inside the loop? Or what is `var`? — Andras Deak -- Слава Україні, Dec 22 '15 at 20:54
Your written out algorithm says radon transform then sobel on the result, your code is doing the reverse. Depending on the colours present in your image, converting RGB to grey may also not be the best idea - perhaps try converting to HSV and then computing for one or more of those channels. — nkjt, Dec 23 '15 at 18:18
My bad. I've adjusted the post. I believe you are supposed to sobel then find radon. But I'm not sure how to apply radon only to the maximum disk area. Is there any way in matlab to extract this area? I used grey because i was following the article. But i will try other color spaces. thank you! — User404, Dec 23 '15 at 18:50
Can you post your source image? Also, I would encourage you to use a lossless image format like png rather than jpg. — beaker, Feb 03 '16 at 16:57
I *think* it's as simple as using a circular mask with a diameter equal to the smallest dimension of the image. The reason I think this is that, as you change the angle of the Radon transform, the extent of the image at each of the angles will be a constant. Unfortunately I was not able to produce the desired results using this method, but I was not able to reproduce your graph above, either. It's possible that this is because I'm using Octave rather than MATLAB, so you might want to give this a try and see what you get. — beaker, Feb 04 '16 at 00:18
@beaker Did your graph show two distinct peaks? because that is really what i'm hoping to produce. And as i mentioned, i was unsure about steps one and two. Are you saying to use a circular mask on the image and then perform radon transform? But would that be the same as perfoming radon transform on the maximum disk area? — User404, Feb 04 '16 at 01:22
That would be my guess and I followed your code otherwise, but no, I didn't get two peaks in the graph. — beaker, Feb 04 '16 at 02:11
@User404 Try your code with this image: http://imgur.com/bA2mmQp — beaker, Feb 04 '16 at 03:25
Yes that gives 2 distinct peaks as it should! so i tried a different edge detetector to get a better binary image, (roberts) and i got slightly better peaks. Thanks. — User404, Feb 04 '16 at 04:01

score 2 · Accepted Answer · edited Feb 10 '16 at 01:04

Maximum disk area is, as @beaker thought, defined by the maximum filled circle that fits inside the bounding box of the image. That you can observe from the Fig.3 b) of the article.

Another thing you did wrong, is using edge detector edge(grey, 'sobel') while you should use gradient map or more formally gradient magnitude. Here's a code which produces a curve close to what is shown in Fig 3d. How to quantify it to six peaks, remains a question.

A = imread( 'Layer-5.png' ); % image from the article
A = double(rgb2gray( A ));

% gradient magnitude
dx = imfilter(A,fspecial('sobel') ); % x, 3x3 kernel
dy = imfilter(A,fspecial('sobel')'); % y
gradmag = sqrt( dx.^2 + dy.^2 );

% mask by disk
R = min( size(A)/2 ); % radius
disk = insertShape(zeros(size(A)),'FilledCircle', [size(A)/2,R] );
mask = double(rgb2gray(disk)~=0);
gradmag = mask.*gradmag;

% radon transform
theta = linspace(0,180,180);
vars = zeros(size(theta));
for u = 1:length(theta)
    [rad,xp] =radon( gradmag, theta(u) );
    indices = find( abs(xp)<R );
    % ignore radii outside the maximum disk area
    % so you don't sum up zeroes into variance
    vars(u) = var( rad( indices ) );
end
vars = vars/norm(vars);
figure; plot( vars );

Bear in mind, images copied from the article appear with jpg artefacts. After good denoising (a tad too much here), e.g.,

you get much more prominent results.

how did you perform the denoising to get this result? – User404 Feb 28 '16 at 02:13 — User404, Feb 28 '16 at 02:13

Image Processing - Using Radon Transform for Pattern Recognition in MATLAB

1 Answers1