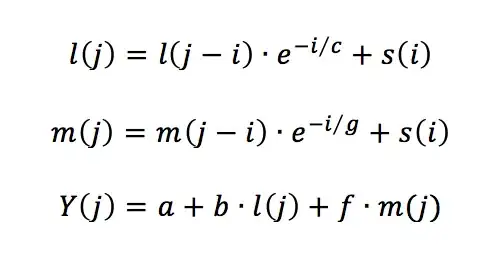This is the function that I'd like to code in R,
i = 1,2,3,....j-1
a,b,c,f,g are to be determined from nls (with starting value arbitrarily set to 7,30,15,1,2)
S and Y are in the dataset
The function can be presented in a more computational friendly recursive equations,
Here is my attempt at the code but I could not get it to converge,
S=c(235,90,1775,960,965,1110,370,485,667,140,588,10,0,1340,600,0,930,1250,930,120,895,825,0,935,695,270,0,610,0,0,445,0,0,370,470,819,717,0,0,60,0,135,690,0,825,730,1250,370,1010,261,0,865,570,1425,150,1515,1143,0,675,1465,375,0,690,290,0,430,735,510,270,450,1044,0,928,60,95,105,60,950,0,1640,3960,1510,500,1135,0,0,0,181,568,60,1575,247,0,1270,870,290,510,0,540,455,120,580,420,90,525,1116,499,0,60,150,660,1080,1715,90,1090,840,975,280,850,633,30,1530,1765,880,150,225,77,1380,810,835,0,540,1017,1108,0,300,600,90,370,910,0,60,60,0,0,0,0,50,0,735,900)
Y=c(NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,NA,7.7,NA,NA,7.2,NA,NA,NA,NA,NA,NA,7.4,NA,NA,NA,NA,NA,NA,10.7,NA,NA,NA,NA,8.1,8.5,NA,NA,NA,NA,NA,9.9,NA,7.4,NA,NA,NA,9.5,NA,NA,9,NA,NA,NA,8.8,NA,NA,8.5,NA,NA,NA,6.9,NA,NA,7.9,NA,NA,NA,7.3,NA,7.9,8.3,NA,NA,NA,11.5,NA,NA,12.3,NA,NA,NA,6.1,NA,NA,9,NA,NA,NA,10.3,NA,NA,9.7,NA,NA,8.6,NA,9.1,NA,NA,11,NA,NA,12.4,11.1,10.1,NA,NA,NA,NA,11.7,NA,NA,9,NA,NA,NA,10.2,NA,NA,11.2,NA,NA,NA,11.8,NA,9.2,10,9.8,NA,9.5,11.3,10.3,9.5,10.2,10.6,NA,10.8,10.7,11.1,NA,NA,NA,NA,NA,NA,NA,NA,12.6,NA)
mydata = data.frame(Y,S)
f <- function(a,b,f,c,g,m) {
model <- matrix(NA,nrow(m)+1,3)
model[1,1]=0
model[1,2]=0
model[1,3]=a
for (i in 2:nrow(model)){
model[i,1]=exp(-1/c)*model[i-1,1] + m$S[i-1]
model[i,2]=exp(-1/g)*model[i-1,2] + m$S[i-1]
model[i,3]=a+b*model[i,1]-f*model[i,2]
}
model <- as.data.frame(model)
colnames(model) = c('l','m','Y')
model$Y[which(m$Y>0)]
}
Y=mydata$Y
nls(Y ~ f(a,b,f,c,g,mydata), start=list(a=7,b=5.3651,f=5.3656,c=16.50329,g=16.5006),control=list(maxiter=1000,minFactor=1e-12))
Errors that I've been getting depends on the starting values are:
Error in nls(Y ~ f(a, b, f, c, g, mydata), start = list(a = 7, :
number of iterations exceeded maximum of 1000Error in nls(Y ~ f(a, b, f, c, g, mydata), start = list(a = 7, :
singular gradient
I'm stuck and not sure what to do, any help would be greatly appreciated.