Categorical and ordinal feature data difference in regression analysis?

Question

I am trying to completely understand difference between categorical and ordinal data when doing regression analysis. For now, what is clear:

Categorical feature and data example:
Color: red, white, black
Why categorical: red < white < black is logically incorrect

Ordinal feature and data example:
Condition: old, renovated, new
Why ordinal: old < renovated < new is logically correct

Categorical-to-numeric and ordinal-to-numeric encoding methods:
One-Hot encoding for categorical data
Arbitrary numbers for ordinal data

Example for categorical:

data = {'color': ['blue', 'green', 'green', 'red']}

Numeric format after One-Hot encoding:

   color_blue  color_green  color_red
0           1            0          0
1           0            1          0
2           0            1          0
3           0            0          1

Example for ordinal:

data = {'con': ['old', 'new', 'new', 'renovated']}

Numeric format after using mapping: Old < renovated < new → 0, 1, 2

0    0
1    2
2    2
3    1

In my data price increases as condition changes from "old" to "new". "Old" in numeric was encoded as '0'. 'New' in numeric was encoded as '2'. So, as condition increases, then price also increases. Correct.
Now lets have a look at 'color' feature. In my case, different colors also affect price. For example, 'black' will be more expensive than 'white'. But from above mentioned numeric representation of categorical data, I do not see increasing dependancy as it was with 'condition' feature. Does it mean that change in color does not affect price in regression model if using one-hot encoding? Why to use one-hot encoding for regression if it does not affect price anyway? Can you clarify it?

UPDATE TO QUESTION:
First I introduce formula for linear regression:
Let have a look at data representations for color: 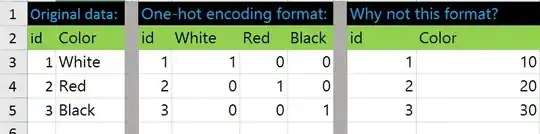Let's predict price for 1-st and 2-nd item using formula for both data representations:
One-hot encoding: In this case different thetas for different colors will exist and prediction will be:

Price (1 item) = 0 + 20*1 + 50*0 + 100*0 = 20$  (thetas are assumed for example)
Price (2 item) = 0 + 20*0 + 50*1 + 100*0 = 50$  (thetas are assumed for example)

Ordinal encoding for color: In this case all colors have common theta but multipliers differ:

Price (1 item) = 0 + 20*10 = 200$  (theta assumed for example)
Price (2 item) = 0 + 20*20 = 400$  (theta assumed for example)

In my model White < Red < Black in prices. Seem to be that it is logical predictions in both cases. For ordinal and categorical representations. So I can use any encoding for my regression regardless of the data type (categorical or ordinal)? This division is just a matter of conventions and software-oriented representations rather than a matter of regression logic itself?

Answer 1

You will see not increasing dependency. The whole point of this discrimination is that colour is not a feature you can meaningfully place on a continuum, as you've already noted.

The one-hot encoding makes it very convenient for the software to analyze this dimension. Instead of having a feature "colour" with the listed values, you have a set of boolean (present / not-present) features. For instance, your row 0 above has features color_blue = true, color_green = false, and color_red = false.

The prediction data you get should show each of these as a separate dimension. For instance, presence of color_blue may be worth $200, while green is -$100.

Summary: don't look for a linear regression line running across a (non-existent) color axis; rather, look for color_* factors, one for each color. As far as your analysis algorithm is concerned, these are utterly independent features; the "one-hot" encoding (a term from digital circuit design) is merely our convention for dealing with this.

Does this help your understanding?

After your edit of the question 02:03 Z 04 Dec 2015:

No, your assumption is not correct: the two representations are not merely a matter of convenience. The ordering of colors works for this example -- because the effect happens to be a neat, linear function of the chosen encoding. As your example shows, your simpler encoding assumes that White-to-Red-to-Black pricing is a linear progression. What do you do when Green, Blue, and Brown are all $25, the rare Yellow is worth $500, and Transparent reduces the price by $1,000?

Also, how is it that you know in advance that Black is worth more than White, in turn worth more than Red?

Consider the case of housing prices based on elementary school district, with 50 districts in the area. If you use a numerical coding -- school district number, ordinal position alphabetically, or some other arbitrary ordering -- the regression software will have great trouble finding a correlation between that number and the housing price. Is PS 107 a more expensive district than PS 32 or PS 15? Are Addington and Bendemeer preferred to Union City and Ventura?

Splitting these into 50 different features under that one-hot principle decouples the feature from the encoding, and allows the analysis software to treat with them in a mathematically meaningful manner. It's not perfect by any means -- expanding from, say, 20 features to 70 means that it will take longer to converge -- but we do get meaningful results for the school district.

If you wish, you could now encode that feature in the expected order of value, and get a reasonable fit with little loss of accuracy and faster prediction from your model (fewer variables).

Answer 2

You cannot use ordinal encoding for a categorical variable where order doesn't matter. Main purpose of building a regression model is to see how much change in one variable has how much effect on the response variable. When you obtain the regression formula this is how you read it: "1 unit change in variable X causes theta_x change in response variable".

For example, let's say you built a regression model on housing prices and you got this: price = 1000 + (-50)*age_of_house. This means 1 year increase in the age of the house causes the price go down by 50.

When you have a categorical variable you cannot mention a unit change in that variable. You cannot say 1 unit increase/decrease in the color... etc. So, one-hot encoding, as Prune said in his/her answer, is merely a convention for dealing with categorical variables. It allows you to interpret the results like, if the house is white it adds $200 to the value when coefficient of color_white in your final model is +200. If the house is not white, that variable has no impact on your response variable because the value will be 0.

Don't forget that "Linear Regression" models can only explain linear relations between variables.

I hope this helps.