-1

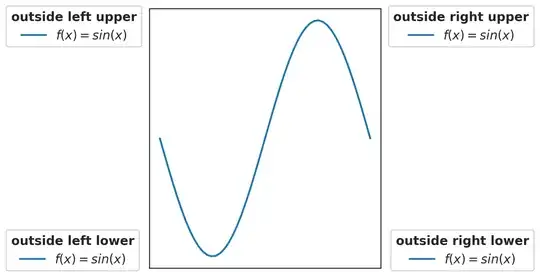
I was given the original sine wave(Image 1) and a noisy version of it too(Image 2).

Image 1

enter image description here

Image 2

enter image description here

Now to find the original signal, I am looking at the frequency in the first half of the graph which has the greatest value. This would be 21. When I try to create a sine wave with 21 as a frequency using the code below, I get the result of Image 3.

% Creating the Sine Wave
t = (1:1:256); 
A = 1; 
y = A*sin(2*pi*max_index*t);

plot(t,y);

Image 3

enter image description here

Why is this the case. What am I doing wrong?

RUNNABLE CODE

Here is my Function: 

function [  ] = function1b( Sig_noise )

% Max Index is the frequency of the pure tone
noise_f = fft(Sig_noise); 
s_nf = size(noise_f);
size_f = s_nf(2); 
max = 0;
max_index = 1; 
for n = 1:(size_f/2)
    if abs(noise_f(n)) > max 
        max = abs(noise_f(n));
        max_index = n; 
    end
end

% Creating the Sine Wave
t = (1:1:256); 
A = 1; 
y = A*sin(2*pi*max_index*t);

plot(t,y);

end

And I am calling it from this part of the script: 

load('Sig'); % Original Signal
Sig_noise2=awgn(Sig,10);
function1b(Sig_noise2);

Andras' Solution

This is the result I seem to be getting:

enter image description here

Using linspace(0,2,100); gives me this result:

enter image description here

SDG
  • 2,260
  • 8
  • 35
  • 77
  • 1
    Can you post some runnable code? To me this looks alright, your amplitude should not change, because A is constant, so no idea why you are getting this output. – lhcgeneva Nov 29 '15 at 11:04
  • @lhcgeneva just made the change! – SDG Nov 29 '15 at 11:23

2 Answers2

2

Your code says

t = (1:1:256); 
A = 1; 
y = A*sin(2*pi*max_index*t);

While your amplitude is nice and big and 1, if max_index is integer then your phase inside the sin is an integer multiple of 2*pi for every t, which is exactly zero. This is why your function is numerically zero. You need the frequency of the max index:

y = A*sin(2*pi*freq(max_index)*t);

if the frequencies are stored in freq, or if max_index already stands for a frequency, then use a denser t mesh, like

t = linspace(1,256,1000);

You might be misinterpreting the output of fft. From help fft:

 For length N input vector x, the DFT is a length N vector X,
 with elements
                     N
       X(k) =       sum  x(n)*exp(-j*2*pi*(k-1)*(n-1)/N), 1 <= k <= N.
                    n=1

 The inverse DFT (computed by IFFT) is given by
                    N
      x(n) = (1/N) sum  X(k)*exp( j*2*pi*(k-1)*(n-1)/N), 1 <= n <= N.
                   k=1

That means that the frequencies are not max_index, but (max_index-1)/N if your original sample has N points. This turns your flawed large frequency into the actual small frequency, solving your issues.

To break it down to you: try

t = 1:256;
y = A*sin(2*pi*(max_index-1)/length(Sig_noise)*t);
Andras Deak -- Слава Україні
  • 33,737
  • 11
  • 83
  • 111
  • `Undefined function or variable 'freq'.` is the error I get when I try to change `y = A*sin(2*pi*max_index*t);` to `y = A*sin(2*pi*freq(max_index)*t);` Let me try your second solution. – SDG Nov 29 '15 at 11:27
  • I've also modified the question so that it holds more info on how I got the value of `max_index`. – SDG Nov 29 '15 at 11:28
  • I've also posted the result of the second solution that you have mentioned. – SDG Nov 29 '15 at 11:42
  • @SharanDuggirala the frequency, in your case `max_index` tells you the number of oscillations in 1 time unit. If your `max_index` is equal to 20, then from `t=0` to `t=1` you have 20 oscillations. That's why you see what you're seeing. Try plotting with `t=linspace(0,2,100)`, a much shorter time scale. – Andras Deak -- Слава Україні Nov 29 '15 at 11:45
  • just added what happens if I modify it in that way. – SDG Nov 29 '15 at 11:49
  • @SharanDuggirala Sorry, 100 was a bit optimistic. I meant something like `t=linspace(0,1,10000)`. That should be smooth. – Andras Deak -- Слава Україні Nov 29 '15 at 11:49
  • what I need is the same graph as the original signal. What do you mean by `N` points? – SDG Nov 29 '15 at 12:02
  • 1
    @SharanDuggirala I refuse to believe that you honestly can't understand what I wrote. See my updated answer............ – Andras Deak -- Слава Україні Nov 29 '15 at 12:08
  • not sure why I'm getting downvoted on this question. Yes, I understand completely now. I was getting confused because of the tighter and looser meshes produced by linspace. This is certainly the right answer! – SDG Nov 29 '15 at 12:58
1

I guess there is some problem in sampling rate. replace 

t=(1:1:256)

with

t = (1:1/(f*3):3)

Here f=max_index =21

Anonymous
  • 336
  • 3
  • 23
  • This is certainly giving me the right graph, but not with the right domain. I need it to range till 256 like the original singal? – SDG Nov 29 '15 at 11:44
  • You can change domain with t=(1:1/(f*3):256). However, graph won't look as image1 due to low frequency. If you zoom it, then you will see see output as Image 1. – Anonymous Nov 29 '15 at 11:49
  • Yeah, I need the exact same graph as **Image 1**. I seem to be getting a different sinewave with a much higher frequency here. – SDG Nov 29 '15 at 12:03