Draw "Squiggly" line along a curve in javascript

Question

This is a bit complicated to describe, so please bear with me.

I'm using the HTML5 canvas to extend a diagramming tool (Diagramo). It implements multiple types of line, straight, jagged (right angle) and curved (cubic or quadratic). These lines can be solid, dotted or dashed.

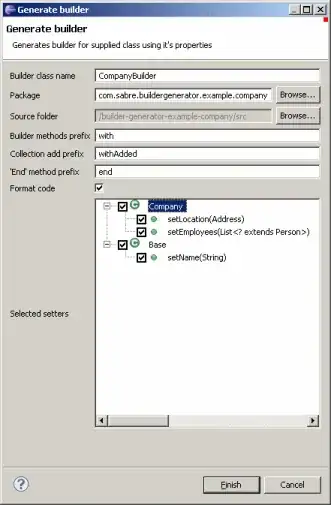
The new feature I am implementing is a "squiggly" line, where instead of following a constant path, the line zigzags back and forth across the desired target path in smooth arcs. Below is an example of this that is correct. This works in most cases, however, in certain edge cases it does not.

The implementation is to take the curve, use the quadratic or cubic functions to estimate equidistance points along the line, and draw squiggles along these straight lines by placing control points on either side of the straight line (alternating) and drawing multiple cubic curves.

The issues occur when the line is relatively short, and doubles back on itself close to the origin. An example is below, this happens on longer lines too - the critical point is that there is a very small sharp curve immediately after the origin. In this situation the algorithm picks the first point after the sharp curve, in some cases immediately next to the origin, and considers that the first segment.

Each squiggle has a minimum/maximum pixel length of 8px/14px (which I can change, but much below that and it becomes too sharp, and above becomes too wavy) the code tries to find the right sized squiggle for the line segment to fit with the minimum empty space, which is then filled by a straight line.

I'm hoping there is a solution to this that can account for sharply curved lines, if I know all points along a line can I choose control points that alternate either side of the line, perpendicular too it?

Would one option be to consider a point i and the points i-1 and i+1 and use that to determine the orientation of the line, and thus pick control points?

Code follows below

//fragment is either Cubic or Quadratic curve.
paint(fragment){
            var length = fragment.getLength();
            var points = Util.equidistancePoints(fragment, length < 100 ? (length < 50 ? 3: 5): 11);
            points.splice(0, 1); //remove origin as that is the initial point of the delegate.
            //points.splice(0, 1);
            delegate.paint(context, points);
}

/**
 *
 * @param {QuadCurve} or {CubicCurbe} curve
 * @param {Number} m the number of points
 * @return [Point] a set of equidistance points along the polyline of points
 * @author Zack
 * @href http://math.stackexchange.com/questions/321293/find-coordinates-of-equidistant-points-in-bezier-curve
 */
equidistancePoints: function(curve, m){
    var points = curve.getPoints(0.001);
    // Get fractional arclengths along polyline
    var n = points.length;
    var s = 1.0/(n-1);
    var dd = [];
    var cc = [];
    var QQ = [];
    function findIndex(dd, d){
        var i = 0;
        for (var j = 0 ; j < dd.length ; j++){
            if (d > dd[j]) {
                i = j;
            }
            else{
                return i;
            }
        }
        return i;
    };

    dd.push(0);
    cc.push(0);
    for (var i = 0; i < n; i++){
        if(i >0) {
            cc.push(Util.distance(points[i], points[i - 1]));
        }
    }
    for (var i = 1 ; i < n ; i++) {
        dd.push(dd[i-1] + cc[i]);
    }
    for (var i = 1 ; i < n ; i++) {
        dd[i] = dd[i]/dd[n-1];
    }

    var step = 1.0/(m-1);

    for (var r = 0 ; r < m ; r++){
        var d =  parseFloat(r)*step;
        var i = findIndex(dd, d);
        var u = (d - dd[i]) / (dd[i+1] - dd[i]);
        var t = (i + u)*s;
        QQ[r] = curve.getPoint(t);
    }

    return QQ;
}

SquigglyLineDelegate.prototype = {
        constructor: SquigglyLineDelegate,
        paint: function(context, points){

            var squiggles = 0;
            var STEP = 0.1;
            var useStart = false;
            var bestSquiggles = -1;
            var bestA = 0;
            var distance = Util.distance(points[0], this.start);
            for(var a = SquigglyLineDelegate.MIN_SQUIGGLE_LENGTH; a < SquigglyLineDelegate.MAX_SQUIGGLE_LENGTH; a += STEP){
                squiggles = distance / a;
                var diff = Math.abs(Math.floor(squiggles) - squiggles);
                if(diff < bestSquiggles || bestSquiggles == -1){
                    bestA = a;
                    bestSquiggles = diff;
                }
            }
            squiggles = distance / bestA;
            for(var i = 0; i < points.length; i++){
                context.beginPath();
                var point = points[i];
                for(var s = 0; s < squiggles-1; s++){
                    var start = Util.point_on_segment(this.start, point, s * bestA);
                    var end = Util.point_on_segment(this.start, point, (s + 1) * bestA);
                    var mid = Util.point_on_segment(this.start, point, (s + 0.5) * bestA);
                    end.style.lineWidth = 1;
                    var line1 = new Line(Util.point_on_segment(mid, end, -this.squiggleWidth), Util.point_on_segment(mid, end, this.squiggleWidth));
                    var mid1 = Util.getMiddle(line1.startPoint, line1.endPoint);
                    line1.transform(Matrix.translationMatrix(-mid1.x, -mid1.y));
                    line1.transform(Matrix.rotationMatrix(radians = 90 * (Math.PI/180)));
                    line1.transform(Matrix.translationMatrix(mid1.x, mid1.y));
                    var control1 = useStart ? line1.startPoint : line1.endPoint;

                    var curve = new QuadCurve(start, control1, end);
                    curve.style = null;
                    curve.paint(context);
                    useStart = !useStart;
                }
                this.start = point;
                context.lineTo(point.x, point.y);
                context.stroke();
            }
        }
    }