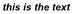Most effecient algorithm for finding this LCM summation

Question

Problem : Find

Range of n : 1<= n <=

The main challenge is handling queries(Q) which can be large . 1 <= Q <=

Methods I have used so far :

Brute Force

while(Q--)
{
    int N;
    cin>>N;
    for(int i=1;i<=N;i++)
        ans += lcm(i,N)/i ;
}

Complexity :

Preprocessing and Handling queries in

First I build a table which holds the value of euler totient function for every N. This can be done in O(N).

void sieve()
{
    // phi table holds euler totient function value
    // lp holds the lowest prime factor for a number
    // pr is a vector which contains prime numbers 
    phi[1]=1;
    for(int i=2;i<=MAX;i++)
    {
        if(lp[i]==0)
        {
            lp[i]=i;
            phi[i]=i-1;
            pr.push_back(i);
        }
        else
        {
            if(lp[i]==lp[i/lp[i]])
                phi[i] = phi[i/lp[i]]*lp[i];
            else phi[i] = phi[i/lp[i]]*(lp[i]-1);
        }
    for(int j=0;j<(int)pr.size()&&pr[j]<=lp[i]&&i*pr[j]<=MAX;j++)
        lp[i*pr[j]] = pr[j];
}

For each query factorize N and add d*phi[d] to the result.

for(int i=1;i*i<=n;i++)
{
   if(n%i==0)
   {
    // i is a factor
    sum += (n/i)*phi[n/i];
    if(i*i!=n)
        {
            // n/i is a factor too
            sum += i*phi[i];
        }
   }
}

This takes O(sqrt(N)) .

Complexity : O(Q*sqrt(N))

Handling queries in O(1)

To the sieve method I described above I add a part which calculates the answer we need in O(NLogN)

for(int i=1;i<=MAX;++i)
{
    //MAX is 10^7
    for(int j=i;j<=MAX;j+=i)
    {
        ans[j] += i*phi[i];
    }
}

This unfortunately times out for the given constraints and the time limit (1 second).

I think this involves some clever idea regarding the prime factorization of N . I can prime factorize a number in O(LogN) using the lp(lowest prime) table built above but I cant figure out how to arrive at the answer using the factorization.

Alexander Kuznetsov · Answer 1 · 2015-11-09T19:45:20.327

0

You can try following algorithm:

lcm(i,n) / i  = i * n / i * gcd(i, n) = n / gcd(i, n)

Now should find sum of numbers n / gcd(i, n).

Lets n = p1^i1 * p2^i2 * p3^j3 where number p1, p2, ... pk is prime.

Number of items n / gdc(i, n) where gcd(i , n) == 1 is phi[n] = n*(p1-1)*(p2-1)*...*(pk-1)/(p1*p2*...*pk), so add to sum n*phi[n].

Number of items n / gdc(i, n) where gcd(i , n) == p1 is phi[n/p1] = (n/p1)*(p1-1)*(p2-1)*...*(pk-1)/(p1*p2*...*pk), so add to sum n/p1*phi[n/p1].

Number of items n / gdc(i, n) where gcd(i , n) == p1*p2 is phi[n/(p1*p2)] = (n/(p1*p2))*(p1-1)*(p2-1)*...*(pk-1)/(p1*p2*...*pk), so add to sum n/(p1*p2)*phi[n/(p1*p2)].

Now answer is the sum

n/(p1^j1*p2^j2*...*pk^jk)  phi[n/(p1^j1*p2^j2*...*pk^jk)]

over all

j1=0,...,i1  
j2=0,...,i2
....  
jk=0,...,ik

Total number of items in this sum is i1*i2*...*ik that is significantly less then O(n).

To calculate this sum you can use a recursion function with free argument initial number, current representation and initial representation:

initial = {p1:i1, p2:i2, ... ,pn:in} 
current = {p1:i1, p2:i2, ... ,pn:in} 
visited = {}

int calc(n, initial, current, visited):
   if(current in visited):
      return 0
   visited add current 
   int sum = 0
   for pj in keys of current:
      if current[pj] == 0:
        continue
      current[pj]--
      sum += calc(n, initial, current)
      current[pj]++  

   mult1 = n 
   for pj in keys of current:
      mult1 /= pj^current[pj]

   mult2 = mult1
   for pj in keys of current:
      if initial[pj] == current[pj]:
         continue
      mult2 = mult2*(pj -1)/pj

   sum += milt1 * mult2
   return sum

edited Nov 09 '15 at 19:45

answered Nov 09 '15 at 15:55

Alexander Kuznetsov

3,062
2
25
29

I thought of this too . Maximum number of primes here can be 8 ( `as 2*3*5*7*11*13*17*19<=10^7`) but couldn't convert this into code . How do I generate all `j's (j1,j2,j3 etc)` here? 8 nested loops ?! Could you add some pseudo code here please. – Sarvagya Nov 09 '15 at 16:15
1

You only pass 2 arguments in the recursive call . Also `for pj in keys of m` what is m here ? – Sarvagya Nov 09 '15 at 16:36
Also find a small mistake: initial value for mult2 should be 0 not n. – Alexander Kuznetsov Nov 09 '15 at 16:42
I cannot figure out what the problem is but this code doesn't produce the desired output . – Sarvagya Nov 09 '15 at 18:34
I update solutions I had mistake in Euler's totient function, also in recursion function was a mistake we should visit again a visited state. I run this solution and coincide with brute force answer. This task is not seems easy as from the first glance. – Alexander Kuznetsov Nov 09 '15 at 19:52
`if(current in visited)` : any idea to implement this in c++? – Sarvagya Nov 09 '15 at 19:57
Sorry I didn't understand you . Also what you are essentially doing is generating factors from the prime factorization and then finding their contribution to the answer . I don't see why this would be any faster than simply finding factors(in O(logN)) and O(N) preprocessing. – Sarvagya Nov 09 '15 at 20:00
Create a function that return from current some unique key, e.g. a string as contact via comma a all values from 'current' map. – Alexander Kuznetsov Nov 09 '15 at 20:09
Let us [continue this discussion in chat](http://chat.stackoverflow.com/rooms/94641/discussion-between-alexander-kuznetsov-and-sarvagya-agarwal). – Alexander Kuznetsov Nov 09 '15 at 20:17

score 0 · Answer 2 · answered Dec 18 '22 at 02:49

Its possible to quickly determine the sum if you know the prime factorization of the number N. Working off the same approach (totient function times N divided by a factor) as the existing answer, but applying some algebra to simplify terms, factor the expression to sums of prime powers, substituting the formula for a geometric series... we arrive at a much simpler solution.

Given the prime factorization of N in primes ps to powers qs, we can compute the result of the original equation for N via:

result = 1
for p, q in prime_factors
    result *= p * (p-1) * (p**(2*q) - 1) / (p**2 - 1) + 1

Note that ** denotes exponentiation in the above pseudo-code.

If one sieves for primes up to MAX, storing at least one prime divisor for each composite discovered (as mentioned in the original problem) as precomputation, its possible to then factor the subsequent N values in log(N) time by referencing the factor table. If one also pre-computes a prime power table, the above algorithm can then run in log(N) time, for an overall complexity of O(MAX*log(MAX)) pre-computing time and O(Q*log(MAX)) query time, and O(MAX) space.

Most effecient algorithm for finding this LCM summation

2 Answers2