In formal, does there exist 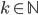 such that
such that 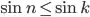 for all
for all 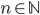 ?
?
Asked
Active
Viewed 432 times
-4
xskxzr
- 12,442
- 12
- 37
- 77
-
This better goes to http://math.stackexchange.com/ – a_guest Oct 15 '15 at 12:50
-
4I'm voting to close this question as off-topic because this is a purely mathematical question (structure of real numbers) and thus belongs to math.se – Lutz Lehmann Oct 15 '15 at 12:51
-
1I'm voting to close this question as off-topic because it is about mathematics, not programming or software development. – Pang Oct 16 '15 at 01:23
1 Answers
2
No, $\pi$ and thus $\pi/2$ are irrational, thus the (additive) equivalence classes of the integers modulo $2\pi$ are dense in $\Bbb R$ and thus approach infinitesimally, but never reach $\pi/2$.
The fundamental fact is that for any given number x the set of numbers {mx+n : m,n integer} is either
an arithmetic sequence {mr : r integer} which implies and is equivalent to x as a multiple of r being rational, or
dense in the real numbers, which by the first case happens for all irrational x.
Lutz Lehmann
- 25,219
- 2
- 22
- 51