How to understand DFT results

Question

I use this implementation of DFT:

/*
Direct fourier transform
*/
int DFT(int dir,int m,double *x1,double *y1)
{
    long i,k;
    double arg;
    double cosarg,sinarg;
    double *x2=NULL,*y2=NULL;

    x2 = malloc(m*sizeof(double));
    y2 = malloc(m*sizeof(double));
    if (x2 == NULL || y2 == NULL)
       return(FALSE);

    for (i=0;i<m;i++) {
       x2[i] = 0;
       y2[i] = 0;
       arg = - dir * 2.0 * 3.141592654 * (double)i / (double)m;
       for (k=0;k<m;k++) {
          cosarg = cos(k * arg);
          sinarg = sin(k * arg);
          x2[i] += (x1[k] * cosarg - y1[k] * sinarg);
          y2[i] += (x1[k] * sinarg + y1[k] * cosarg);
       }
    }

    /* Copy the data back */
    if (dir == 1) {
      for (i=0;i<m;i++) {
         x1[i] = x2[i] / (double)m;
         y1[i] = y2[i] / (double)m;
      }
   } else {
      for (i=0;i<m;i++) {
         x1[i] = x2[i];
         y1[i] = y2[i];
      }
   }

   free(x2);
   free(y2);
   return(TRUE);
}

Which is placed here http://paulbourke.net/miscellaneous/dft/

First question is why after applying direct transform(dir=1) we should scale values? I read some ideas about DFT implementation and didn't find anything about it.

As input I use cos with 1024 sampling frequency

#define SAMPLES 2048
#define ZEROES_NUMBER 512

double step = PI_2/(SAMPLES-2*ZEROES_NUMBER);
for(int i=0; i<SAMPLES; i++)
{
    /*
     * Fill in the beginning and end with zeroes 
     */
    if(i<ZEROES_NUMBER || i > SAMPLES-ZEROES_NUMBER)
    {
        samplesReal[i] = 0;
        samplesImag[i] = 0;
    }
    /*
     *  Generate one period cos with 1024 samples
     */
    else
    {
        samplesReal[i] = cos(step*(double)(i-ZEROES_NUMBER));
        samplesImag[i] = 0;
    }
}

For plotting I removed scaling about which I asked above because output values become very small and it's impossible to plot graph.

And I got such graphs of amplitude and phase:

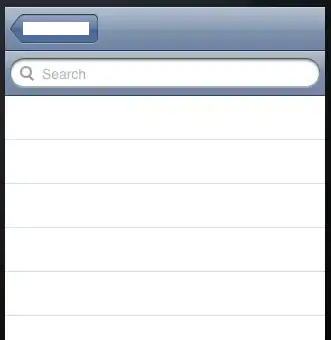
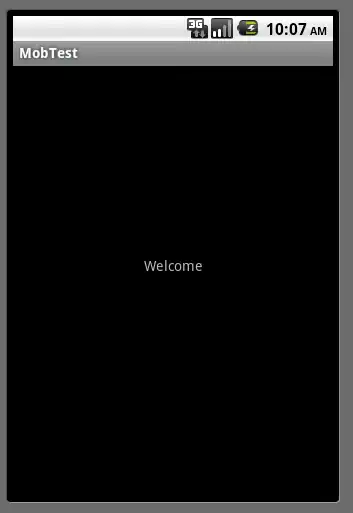
As you can see phase is always 0 and amplitude spectrum is reversed. Why?

Below is my more readable version without scaling which produces the same result:

void DFT_transform(double complex* samples, int num, double complex*   res)
{
    for(int k=0; k<num; k++)
    {
        res[k] = 0;
        for(int n=0; n<num; n++)
        {
            double complex Wkn = cos(PI_2*(double)k*(double)n/(double)num) -
            I*sin(PI_2*(double)k*(double)n/(double)num);

            res[k] += samples[n]*Wkn;
        }
    }
}

@LightnessRacesinOrbit my implementation uses complex library which is written in c++. — Long Smith, Oct 08 '15 at 10:51
One question per question please. Scaling is just a convention, and there are different conventions - typically it's 1/N in the forward direction and no scaling in the reverse direction. To see if your DFT is working correctly start with a purely real sine wave and look at the *magnitude* of your output bins (sqrt(re^2 + im^2)). — Paul R, Oct 08 '15 at 10:53
@PaulR thanks. I tried as input `cos(i)`. That's what I got for [amplitude](http://s017.radikal.ru/i439/1510/5b/cb9b6f87c408.jpg) and [phase](http://s017.radikal.ru/i408/1510/5a/531777335ea9.jpg). Amplitude is just a little bit different but in phase appeared something new. That was with filling zeroes in the beginning and end. — Long Smith, Oct 08 '15 at 11:05
@LongSmith: by amplitude do you mean magnitude, i.e. `sqrt(re^2 + im^2)` ? Note that the input should have e.g. a sine wave in x1 and zeroes in y1 - don't pad the beginning and end with zeroes as you have in the code in your question. You can check you results against a known good DFT or FFT implementation, e.g. Octave (free MATLAB clone). — Paul R, Oct 08 '15 at 11:22
@PaulR yes, by amplitude I mean magnitude, sorry for mess. Here is graph for [magnitude](http://s017.radikal.ru/i405/1510/10/64eded8318fd.jpg) and [phase](http://s018.radikal.ru/i527/1510/c3/2584ed5979b3.jpg) without zeroes. They display something weird. Will try MATLAB later. — Long Smith, Oct 08 '15 at 11:38
I think perhaps your sine wave is a very low frequency, relative to the DFT bin resolution - try increasing the frequency by an order of magnitude, e.g. sin(2 * PI * 10 * i / n) - that should give you a magnitude peak around bin 10. — Paul R, Oct 08 '15 at 13:48

Long Smith · Accepted Answer · 2015-10-09T19:01:09.513

Ok, guys. I'm glad to say that this implementation works. Problem was the wrong way of plotting graphs and a lack of understanding formulas.

How it works

As you can see there is k variable which is used to vary the frequency. So frequency is ν = k / T where T is a period of time taken to get samples. T = N/S where S is your sampling frequency. Then you can find your frequency as v = S*k/N

So when you get your result you should calculate frequencies for each point and remove everything that above S/2 and only then plot graph Magnitude = Magnitude(Frequency). This is what I didn't understand before. Hope it will be helpful to someone.

Some graphs I got.

Sin 100HZ.

Sin 100HZ + Cos 200HZ.

Sin 100HZ + (Cos 200HZ)/2

As you can see frequencies and related magnitudes are shown. There is a problem with scaling but it doesn't matter if we want to determine frequencies presented in a signal.

Thanks to @PaulR

How to understand DFT results

1 Answers1

How it works

Some graphs I got.