Find All Numbers in Array which Sum upto Zero

Question

Given an array, the output array consecutive elements where total sum is 0.

Eg:

For input [2, 3, -3, 4, -4, 5, 6, -6, -5, 10],

Output is [3, -3, 4, -4, 5, 6, -6, -5]

I just can't find an optimal solution.

Clarification 1: For any element in the output subarray, there should a subset in the subarray which adds with the element to zero.

Eg: For -5, either one of subsets {[-2, -3], [-1, -4], [-5], ....} should be present in output subarray.

Clarification 2: Output subarray should be all consecutive elements.

Answer 1

Here is a python solution that runs in O(n³):

def conSumZero(input):
    take = [False] * len(input)

    for i in range(len(input)):
        for j in range(i+1, len(input)):
            if sum(input[i:j]) == 0:
                for k in range(i, j):
                    take[k] = True;

    return numpy.where(take, input)

EDIT: Now more efficient! (Not sure if it's quite O(n²); will update once I finish calculating the complexity.)

def conSumZero(input):
    take = [False] * len(input)
    cs = numpy.cumsum(input)
    cs.insert(0,0)

    for i in range(len(input)):
        for j in range(i+1, len(input)):
            if cs[j] - cs[i] == 0:
                for k in range(i, j):
                    take[k] = True;

    return numpy.where(take, input)

The difference here is that I precompute the partial sums of the sequence, and use them to calculate subsequence sums - since sum(a[i:j]) = sum(a[0:j]) - sum(a[0:i]) - rather than iterating each time.

Answer 2

Why not just hash the incremental sum totals and update their indexes as you traverse the array, the winner being the one with largest index range. O(n) time complexity (assuming average hash table complexity).

       [2, 3, -3, 4, -4, 5, 6, -6, -5, 10]
sum  0  2  5   2  6   2  7  13  7   2  12

The winner is 2, indexed 1 to 8!

To also guarantee an exact counterpart contiguous-subarray for each number in the output array, I don't yet see a way around checking/hashing all the sum subsequences in the candidate subarrays, which would raise the time complexity to O(n^2).

Answer 3

Based on the example, I assumed that you wanted to find only the ones where 2 values together added up to 0, if you want to include ones that add up to 0 if you add more of them together (like 5 + -2 + -3), then you would need to clarify your parameters a bit more.

The implementation is different based on language, but here is a javascript example that shows the algorithm, which you can implement in any language:

var inputArray = [2, 3, -3, 4, -4, 5, 6, -6, -5, 10];
var ouputArray = [];

for (var i=0;i<inputArray.length;i++){
    var num1 = inputArray[i];

    for (var x=0;x<inputArray.length;x++){
        var num2 = inputArray[x];
        var sumVal = num1+num2;
        if (sumVal == 0){
            outputArray.push(num1);
            outputArray.push(num2);

        }

    }
}

Answer 4

Is this the problem you are trying to solve?

Given a sequence , find 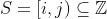maximizing such that

If so, here is the algorithm for solving it:

let $U$ be a set of contiguous integers
for each contiguous $S\in\Bbb Z^+_{\le n}$
    for each $\T in \wp\left([i,j)\right)$
      if $\sum_{n\in T}a_n = 0$
        if $\left|S\right| < \left|U\left$
          $S \to u$

return $U$

(Will update with full latex once I get the chance.)