Question
In R, I would like to create n variables of length L which relationship is given by a correlation matrix called cor_matrix. The important point is that the n variables may follow different distributions (including continuous vs discrete distributions).
Related posts
Modified from the third post listed above, the following is a solution whenever all n variables are continuous and come from the same distribution.
library(psych)
set.seed(199)
fun = function(cor_matrix, list_distributions, L)
{
n = length(list_distributions)
if (ncol(cor_matrix) != nrow(cor_matrix)) stop("cor_matrix is not square")
if (nrow(cor_matrix) != n) stop("the length of list_distributions should match the number of columns and rows of cor_matrix")
if (L<=1) stop("L should be > 1")
fit = principal(cor_matrix, nfactors=n, rotate="none")
loadings = matrix(fit$loadings[1:n, 1:n], nrow=n,ncol=n,byrow=F)
cases = t(sapply(1:n, FUN=function(i, L) list_distributions[[i]](L), L=L))
multivar = loadings %*% cases
T_multivar = t(multivar)
vars=as.data.frame(T_multivar)
return(vars)
}
L = 1000
cor_matrix = matrix(c (1.00, 0.90, 0.20 ,
0.90, 1.00, 0.40 ,
0.20, 0.40, 1.00),
nrow=3,ncol=3,byrow=TRUE)
list_distributions = list(function(L)rnorm(L,0,2), function(L)rnorm(L,10,10), function(L) rnorm(L,0,1))
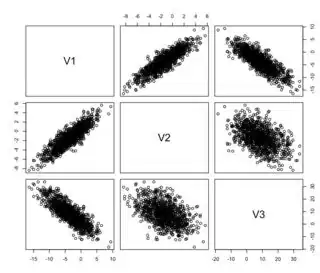
vars = fun(cor_matrix, list_distributions, L)
cor(vars)
plot(vars)
However, one cannot create correlated variables with the following distributions
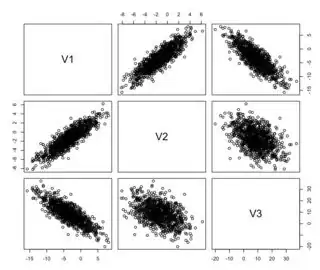
list_distributions = list(function(L)rnorm(L,0,2), function(L)round(rnorm(L,10,10)), function(L) runif(L,0,1))
vars = fun(cor_matrix, list_distributions, L)
cor(vars)
plot(vars)