Let's say I have the following unweighted, undirected graph where edges can be connected by two different types of edges: support edges (green) and opposition edges (red).
Here's an example:
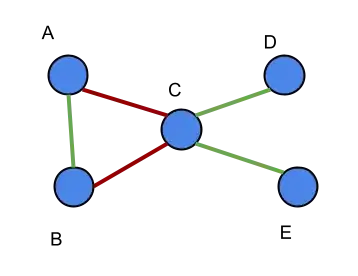
I want to calculate the "distance" of opposition or support between any given two nodes. For example, if the nodes represented countries at war or political candidates, even though A and D have no edge between them we might conclude that they are likely to be opposed to one another since A is opposed to C and C supports D.
This is a simple example, but given a large graph with many nodes of high degree, how might I determine how likely any two nodes might be opposed to or supporting one another if they cannot be directly connected by a successive chain of opposition/support edges?
I imagine you'd represent each node as a vector whose components where whether an edge of a type exist between any other nodes. If this is a good way to go, what distance measure would you use (Euclidean, Hamming, etc?)